참고

  1. 논문



논문의 세세한 내용보다는 네트워크 구조 등을 정리해야지..


You Only Look Once: Unified, Real-Time Object Detection

CVPR 2016

Introduction

Object detection을 single regression

Screenshot from 2024-05-30 19-27-00

YOLO는 그림에서와 같이 간단히게 다음 3가지 단계로 bouding box를 찾는 것이 가능

  1. 이미지 사이즈 조절
  2. Convolutional Network 통과
  3. NMS

YOLO는 하나의 convolution network로 동시에 여러 bounding box들과 그 box들의 class 예측

또한 전체 이미지를 학습하고 직접적으로 detection 성능을 최적화

이 통합된 모델은 몇 가지 장점 존재


첫째, YOLO는 매우 빠른 알고리즘

Regression 문제이기 때문에 기존의 방법과 같이 복잡한 파이프라인 필요 없ㄷ음

테스트 단계에서 새로운 이미지를 YOLO 에 입력으로 넣어주면 쉽게 검출 가능


둘째, YOLO는 예측할 때, 이미지 전체에 대하여 예측

Sliding window나 region proposal 방식과 달리, 학습과 추론 시에 이미지 전체를 보기 때문에 class와 모양(appearance)에 대한 contextual 정보를 인코딩 가능

Fast R-CNN 은 주변 정보까지 (larget context)를 사용하지 못하기 때문에 background의 patch를 object라고 잘못 검출하는 경우가 발생


셋째, object에 대한 일반적인 특징 학습

그렇기 때문에 새로운 도메인의 데이터나 예상하지 못한 입력 데이터가 들어와도 다른 알고리즘보다 roubust 함


빠르게 검출이 가능하지만 기존의 SOTA 알고리즘보다는 정확도가 낮다는 단점

특히 작은 물체에 대한 정확한 localize 정확도가 낮음



Unified Detection

1

입력 image를 $S \times S$ gird로 나누고 나누어진 공간을 cell 이라고 함

  • 이 논문에서 $S=7$

Object의 중심이 grid의 cell 안에 존재하면, 그 cell에서 물체를 detect 해야 함


각 cell에서 Bounding Box 예측

2

각 grid cell은 $B$개의 bounding box와 각 box에 대한 confidence score 예측

  • 논문에서 $B=2$

Confidence score = $Pr(Object) * IOU^{truth}_{pred}$ 라고 정의

Cell에 object가 존재하지 않는다면 confidence score는 0


각 bounding box는 5개의 예측값으로 구성

  • $(x,y)$ : Bounding box의 중심 좌표값, grid cell 내의 상대 위치
  • $(w,h)$ : Bounding box의 너비, 높이
  • Confidence score


즉, 정리하자면 $7\times 7=49$ 개의 cell이 존재하고, 각 cell 마다 2개의 bounding box가 존재하므로 총 $49\times 2=98$ 개의 box 존재

그리고 각 box마다 5개의 값을 예측


각 Cell에서 class 별 확률 예측

각 cell은 conditional class probability $C$를 예측

즉, 각 Cell은 물체가 존재할 때, 어떤 class인지 조건부 확률값 $Pr(Class_{i} Object)$ 계산

3

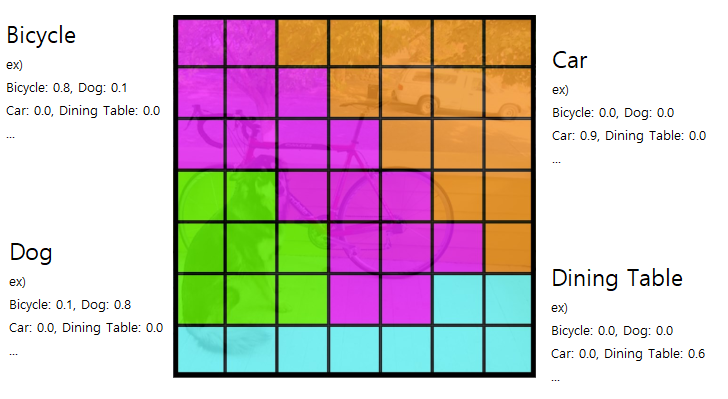
Bounding Box $B$의 수와 상관없이 각 cell의 class 확률을 계산


추론시에는 conditional class probability 값과 예측한 각 box의 confidence를 곱함

\[Pr(Class_{i}|Object)*Pr(Object)*IOU_{pred}^{truth}=Pr(Class_{i})*IOU_{pred}^{truth}\]

이를 통해 box에 대한 class 별 confidence score 를 알 수 있음

이는 각 box에 존재하는 특정 class의 object가 존재할 확률과 box를 object 위치, 크기에 잘 맞게 검출했는지 나타냄


전체 과정

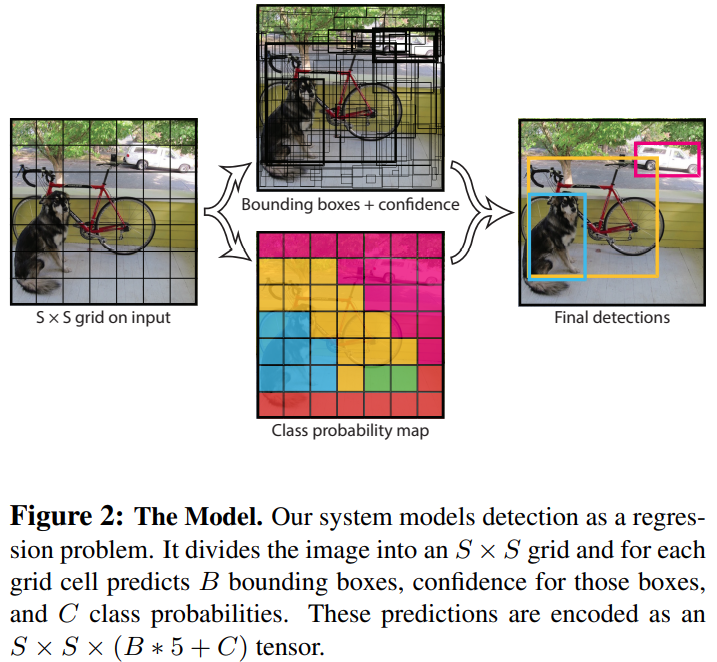
Screenshot from 2024-05-30 22-52-25

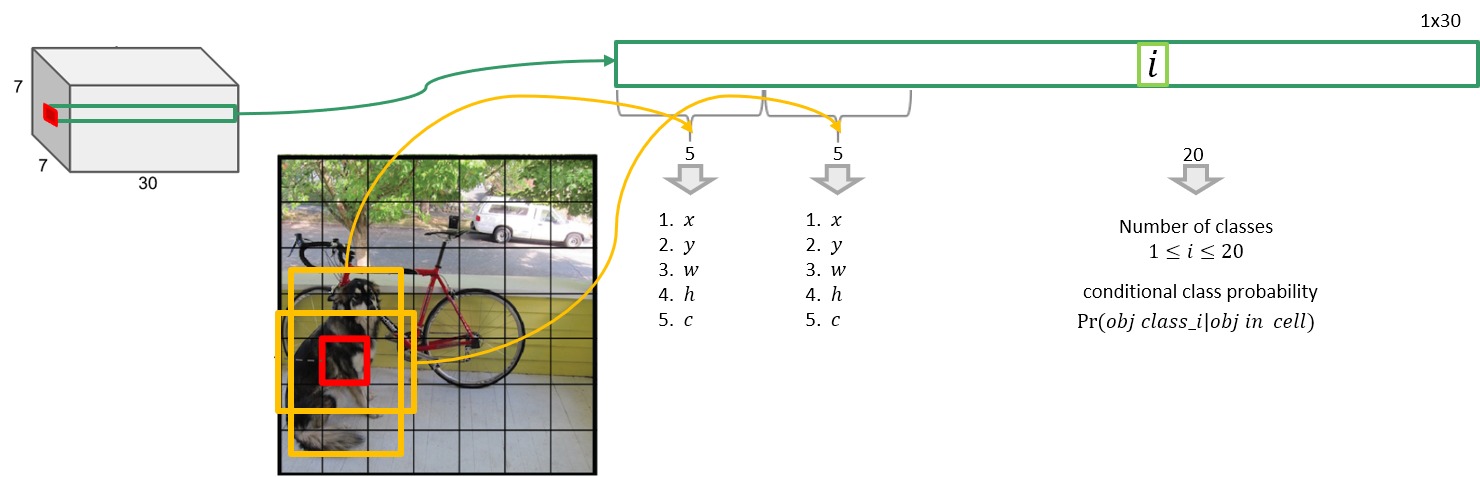
PASCAL VOC 데이터 셋을 이용해서 실험을 진행

$S=7$, $B=2$, VOC가 20개의 class를 가지므로 $C=20$ 으로 설정

이 경우 $S \times S\times (B*5+C)$ 모양의 tensor, 즉 $7\times 7\times 30$ 크기의 tensor가 최종 예측값


4


Network Design

24개의 Convolution layer를 지난 후, 2개의 fully-connected layer를 지나는 네트워크

Screenshot from 2024-05-30 23-14-06


Training

앞단의 20개의 layer들은 backbone으로 224×224 크기 이미지넷 데이터셋으로 pretrain

뒤에 4개의 convolution layer와 2개의 fully-connected layer 추가하여 성능 향상하고 추가시 가중치 임의로 초기화

즉, 학습시 backbone 레이어들은 고정 시키고 나머지 convolution layer들을 object detection task에 맞춰 transfer learning

이 때 입력 이미지의 해상도를 224 x 224에서 448 x 448로 증가


마지막 layer는 class 확률과 bounding box의 좌표($x,y,w,h$)를 예측

Bounding box의 width와 height는 전체 이미지 width, height 기준의 비율로 normalize하여 0 ~ 1사이의 살수값을 사용

좌표값은 특정 gird cell 위치의 offset이 되어 0과 1사이의 값이 됨


Activation Function으로 Leaky ReLU 사용하고 마지막 layer만 linear activation function 적용


학습 시에 사용하는 Loss function은 다음과 같음


\[\begin{split} L_{total}= & \lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbf{1}_{ij}^{\text{obj}} \left[ (x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2 \right] \\ & +\lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbf{1}_{ij}^{\text{obj}} \left[ (\sqrt{w_i} - \sqrt{\hat{w}_i})^2 + (\sqrt{h_i} - \sqrt{\hat{h}_i})^2 \right] \\ & + \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbf{1}_{ij}^{\text{obj}} (C_i - \hat{C}_i)^2 \\ & + \lambda_{\text{noobj}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbf{1}_{ij}^{\text{noobj}} (C_i - \hat{C}_i)^2 \\ & + \sum_{i=0}^{S^2} \mathbf{1}_i^{\text{obj}} \sum_{c \in \text{classes}} (p_i(c) - \hat{p}_i(c))^2 \end{split}\]
  • \(\mathbf{1}_{i}^{\text{obj}}\) : $i$ 번째 cell에 object가 있는 경우를 나타냄
    • 지시함수, 즉 존재하면 1, 존재하지 않으면 0
  • \(\mathbf{1}_{ij}^{\text{obj}}\) : $i$ 번째 cell 안에 $j$ 번째 bounding box에 object가 존재하는 경우
    • 지시함수, 즉 존재하면 1, 존재하지 않으면 0
  • \(\mathbf{1}_{ij}^{\text{noobj}}\) : $i$ 번째 cell 안에 $j$ 번째 bounding box에 object가 존재하지 않는 경우
    • 지시함수, 즉 존재하면 0, 존재하지 않으면 1


첫 번째 loss는 bounding box의 localization error

\[\lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbf{1}_{ij}^{\text{obj}} \left[ (x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2 \right]\\ + \lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbf{1}_{ij}^{\text{obj}} \left[ (\sqrt{w_i} - \sqrt{\hat{w}_i})^2 + (\sqrt{h_i} - \sqrt{\hat{h}_i})^2 \right]\]

Grid cell $i$에 존재하는 $j$ bounding box에 object가 존재하면 좌표값과 크기에 대하여 SSE 를 구함

이 때, SSE는 큰 box와 작은 box에 같은 가중치를 부여한다는 문제가 존재.

Box의 사이즈가 큰 경우는 작은 편차가 작은 box보다 중요하지 않음

즉, 똑같이 10cm를 움직이더라도 box 사이즈가 작으면 영향을 더 받음…

그래서 이를 반영하기 위해 루트를 적용

또한 SSE는 localization error와 classification error에 같은 가중치를 부여하는데 이를 해결하기 위해 $\lambda_{coord}=5$ 라는 값을 곱해 localization 학습이 잘 될 수 있도록 함


두 번째 loss 는 confidence score error

\[\sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbf{1}_{ij}^{\text{obj}} (C_i - \hat{C}_i)^2 \\ + \lambda_{\text{noobj}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbf{1}_{ij}^{\text{noobj}} (C_i - \hat{C}_i)^2\]

이미지 내 대부분의 gird cell에는 detect하고자 하는 object가 존재하지 않음

이런 cell들의 confidence score 예측 값은 0에 가까워지고, 이는 object가 존재하는 grid의 gradient를 압도함

즉, 배경 영역에 대한 confidence가 0에 가까워지는것이 학습을 방해하여 object가 있는 grid cell에 대한 confidence를 감소시킬 수 있음

이를 해결하기 위해 object가 존재하지 않는 경우, $\lambda_{noobj}=0.5$ 라는 가중치를 주어서 학습에 영향을 덜 미치도록 함

즉, grid cell $i$에 존재하는 $j$ bounding box에 object가 존재하면 confidence score에 대한 SSE를 구하고 존재하지 않으면 가중치 값을 곱하여 SSE를 구함

모든 bounding box에 대하여 confidence score가 존재하는데 왜 $C_{i}$인 것일까?


마지막 loss는 classification loss

\[\sum_{i=0}^{S^2} \mathbf{1}_i^{\text{obj}} \sum_{c \in \text{classes}} (p_i(c) - \hat{p}_i(c))^2\]

$i$ 번째 cell에 object가 존재하는 경우에만 각 class 확률에 대한 SSE 계산



Experiments

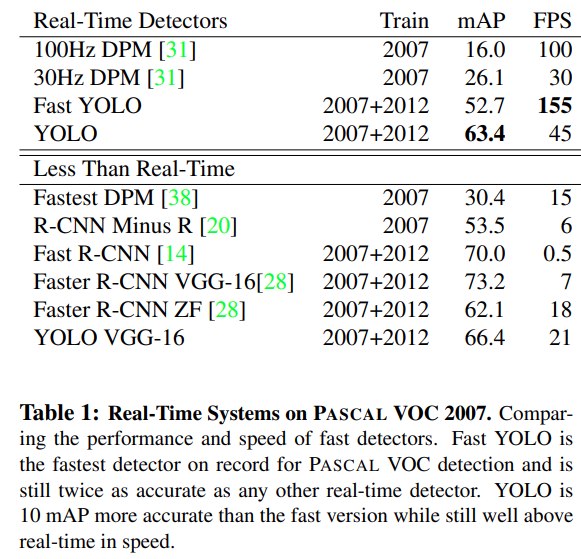
Screenshot from 2024-05-31 01-31-34

  • Real time에 들어가는 알고리즘 중에서는 가장 성능이 좋음
  • Faster R-CNN가 성능이 더 좋지만 FPS가 많이 떨어져서 실시간으로 사용이 어려움


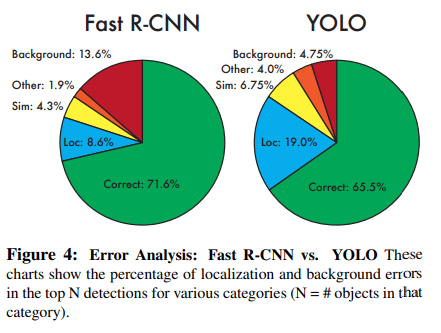
Screenshot from 2024-05-31 01-38-45

  • Localization error는 Yolo가 더 큼
  • Background error는 Fast R-CNN이 더 큼

참고