참고

  1. 논문



Objects as Points

2019

Introduction

기존의 방법과 다르게 object를 bounding box의 중심으로 나타냄

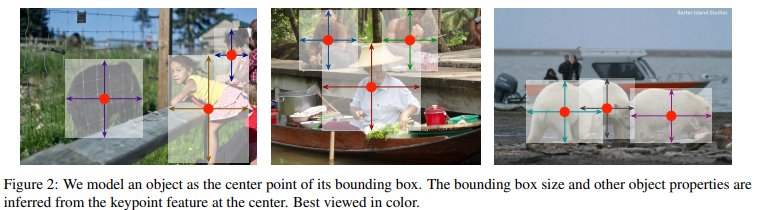
Screenshot from 2024-05-27 23-02-34

Object 크기, 차원, 3D 확장, 방향, 포즈 등의 속성들의 center location의 특징에서 직접적으로 regression하여 획득

이미지를 fully-connected network의 입력으로 사용하여 heatmap 생성하고, 이 heatmap의 peak는 object의 center를 의미

각 peak에서의 feature는 object bounding box의 height, width를 예측함

모델의 학습은 standard dense supervised learning 으로 진행이되고 추론은 post-processing을 위한 NMS 없이 하나의 network forward-pass로 진행


이런 방법은 일반적이고 그렇기 때문에 다른 task로 쉽게 확장 할 수 있음

이 논문에서는 각 center point에서 추가적인 output을 예측하여 3D object detection 과 multi-person human pose estimation의 실험 결과를 제시함


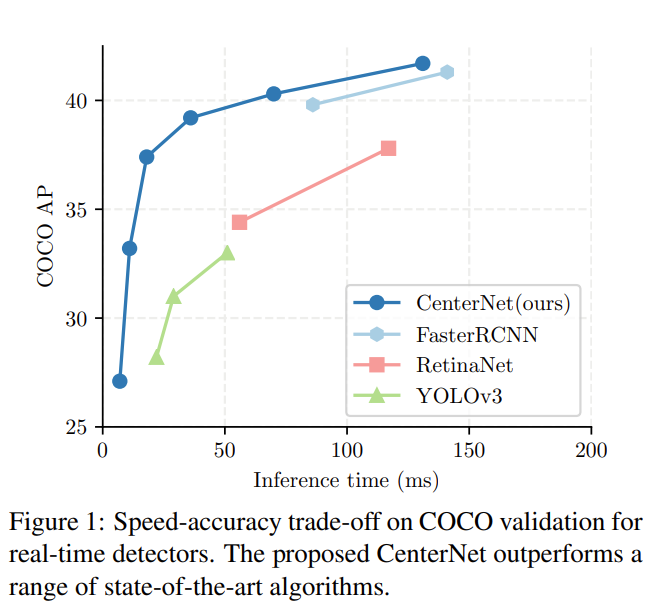
우리가 제시하는 방법인 CenterNet은 단순하고 매우 빠른 추론 속도를 가짐


Screenshot from 2024-05-27 15-52-00



Preliminary

Width가 $W$, height가 $H$ 인 input image를 $I\in R^{W\times H\times 3}$ 로 나타냄

우리의 목표는 keypoint heatmap $\hat{Y}\in [0,1]^{\frac{W}{R}\times \frac{H}{R}\times C }$을 생성 (추정) 하는 것

이 때, $R$은 output stride이고, $C$는 keypoint type의 수

Human pose estimation에서는 joint 수인 $C=17$이고 coco dataset을 이용한 object detection에서는 object의 category 수 (=class 수) 인 $C=80$

Output stride는 $R=4$ 를 default 값으로 사용하고 이를 이용해 output을 downsampling

\(\hat{Y}_{xyc}=1\) 이면 center point, $\hat{Y}_{xyc}=0$ 이면 background 임을 의미

몇 개의 다른 fully-convolutional encoder-decoder network를 이용하여 $\hat{Y}$를 예측

  • Stacked hourglass network, Upconvolutional residual networks (ResNet), Deep layer aggregation (DLA)


Keypoint detection network의 학습은 CornerNet 을 따름

Class $c$에 대한 각 ground truth point ($p\in R^{2}$) 가 있을 때, low-resolution equivalent $\tilde{p}=[\frac{p}{R}]$ 을 계산

그 후, 모든 ground point에 Gaussian kernel을 적용하고($Y_{xyc}$) heapmap $Y \in [0, 1]^{\frac{W}{R}\times \frac{H}{R}\times C }$ 을 생성

즉, ground truth에 전처리를 하여 학습이 더 잘 되게 반영

\[Y_{xyc}=exp(-\frac{ (x-\tilde{p}_{x})^{2}+(y-\tilde{p}_{y})^{2} }{2\sigma^{2}_{p}})\]
  • $\sigma_{p}$ : object size에 adaptive 한 표준 편차

같은 class의 두 Gaussian이 겹치면 element-wise maximum을 계산

Loss 함수는 다음과 같은 focal loss 사용하여 penalty-reduced pixelwise logistic regression

\[L_{k}= \frac{-1}{N}\sum_{xyc} \left\{\begin{aligned} &(1-\hat{Y}_{xyc})^{\alpha}\log(\hat{Y}_{xyc}), \ if \ Y_{xyc}=1 \\ &(1-Y_{xyc})^{\beta}(\hat{Y}_{xyc})^{\alpha}\log(1-\hat{Y}_{xyc}), \ otherwise \end{aligned}\right.\]
  • $\alpha$, $\beta$ : hyper-parameter
  • $N$ : Image $I$ 의 keypoint 수

N 으로 정규화하면 모든 positive focal loss instance를 1이 됨


Output stride로 발생한 discretization error을 헤결하기 위해 각 center point에서 추가적으로 local offset \(\hat{O}\in R^{\frac{W}{R}\times \frac{H}{R}\times C }\) 예측

Center point는 4배 downsampling 된 resolution의 feature에서 에측한 결과이고 이를 다시 input image의 resolution에 대응되게 만들어야 함

모든 class $c$ 들은 같은 offset prediction 공유하고, L1 loss로 학습

\[L_{off}=\frac{1}{N}\sum_{p} |\hat{O}_{\tilde{p}}-(\frac{p}{R}-\tilde{p})|\]

Keypoint $\tilde{p}$에 대해서만 supervision acts이 진행이 되고 다른 location에서는 무시됨



Objects as Points

Category $c_{k}$의 object $k$의 bounding box는 \((x_{1}^{(k)}, y_{1}^{(k)}, x_{2}^{(k)}, y_{2}^{(k)})\) 이고, center point $p_{k}$는 \((\frac{x_{1}^{(k)}+x_{2}^{(k)}}{2}, \frac{y_{1}^{(k)}+ y_{2}^{(k)}}{2})\)

Keypoint estimator $\hat{Y}$을 모든 center point를 예측하기 위해 사용

각 Object $k$에 대해서 object size \(s_{k}=(x_{2}^{(k)}-x_{1}^{(k)},y_{2}^{(k)}- y_{1}^{(k)})\)을 regression

계산의 부담을 줄이기 위해, 모든 object category에 대해서 single size에 대한 예측 $\hat{S}\in R^{\frac{W}{R}\times \frac{H}{R}\times C }$ 을 사용

  • Low resolution에서 single size에 대하여 예측

L1 loss를 사용하여 학습

\[L_{size}=\frac{1}{N}\sum_{k=1}^{N}|\hat{S_{p_k}}-s_{k}|\]


Scale을 normalize 하지 않고 직접적으로 raw pixel coordinate을 사용

전체적인 학습 objective는 아래와 같음

\(L_{det}=L_{k}+\lambda_{size}L_{size}+\lambda_{off}L_{off}\)

Keypoint $\hat{Y}$, offset $\hat{O}$, size $\hat{S}$를 예측하기 위해서 하나의 네트워크를 사용

네트워크는 각 location마다 $C+4$의 output을 가지고 모든 output은 fully-convolutional backbone network를 공유함


Screenshot from 2024-05-27 18-44-47


From points to bounding boxes

추론 할 때, 우선 각 category에서 독립적으로 heatmap의 peak들을 찾음

값이 8-connected neighbor보다 크거나 같은 모든 response(중간값이라고 생각)를 찾고, 가장 큰 100개의 peak를 저장

$\hat{P}_{c}$는 $n$개의 detection한 class $c$에 대한 center point \(\hat{P}=\{(\hat{x}_{i},\hat{y}_{i}) \}^{n}_{i=1}\)의 집합

각 keypoint location은 정수인 좌표 $(x_{i}, y_{i})$ 로 나타냄

Key point value인 \(\hat{Y}_{x_{i}y_{i}c}\)를 detection confidence를 측정하고, bounding box를 측정하는데 사용

  • Heatmap을 이용하여 confidence 측정

Boudning box는 아래와 같이 나타냄

\[(\hat{x}_{i}+\delta\hat{x}_{i}-\hat{w}_{i}/2, \hat{y}_{i}+\delta\hat{y}_{i}-\hat{h}_{i}/2 \\ \hat{x}_{i}+\delta\hat{x}_{i}+\hat{w}_{i}/2, \hat{y}_{i}+\delta\hat{y}_{i}-\hat{h}_{i}/2 ) \\\]
  • \((\delta\hat{x}_{i}, \delta\hat{y}_{i})=\hat{O}_{\hat{x}_{i},\hat{y}_{i}}\) : offset prediction
  • \((\hat{w}_{i}), \hat{h}_{i}=\hat{S}_{\hat{x}_{i}}, \hat{y}_{i}\) : size prediction

모든 output들은 IoU 기반의 NMS 방식을 사용하지 않고 keypoint estimation에서 직접적으로 얻음



Implementation detailsf

4 가지 아키텍쳐에 대하여 실험을 진행

  • ResNet-18, ResNet101, DLA-34, Hourglass-104


Hourglass

Stacked Hourglass Network 는 2개의 연속된 hourglass module을 지나면서input을 4배 downsampling

이 네트워크는 크지만, 일반적으로 가장 좋은 keypoint estimation 성능을 도출


ResNet

Simple baseline에서는 standard residual network에 3개의 up-convolution network를 추가하여 higher-resolution output 생성

CenterNet에서는 3개의 upsampling layer의 채널을 각각 256, 128, 64로 바꿈

  • 계산량을 줄이기 위해

각 up-convolution layer 전에 하나의 3 $\times$ 3 deformable convolution layer를

추가

Up-convolutoion kernel은 bilinear interpolation으로 초기화


DLA

Deep Layer Aggregation (DLA) 는 hierarchical skip connections을 가지는 image classification network

Dense한 prediction을 위해 DLA의 fully convolutional upsampling 사용

매 upsampling layer에 3$\times$3 deformable convolution을 적용



Experiments

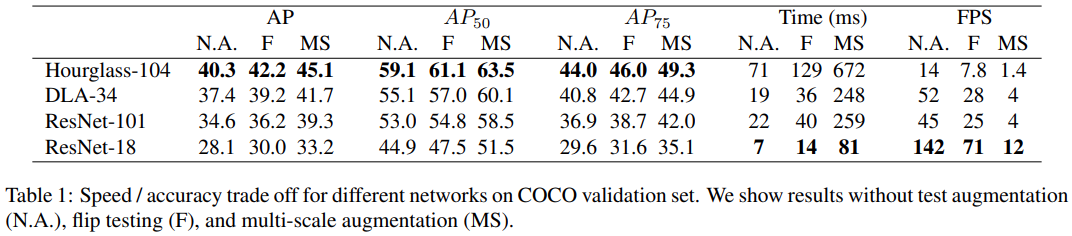
Screenshot from 2024-05-27 22-33-09

  • Hourglass-104가 가장 좋은 성능을 보임을 확인
    • 이 때, CornerNet 과 and ExtremeNet 보다 속도와 정확도가 더 좋음을 확인
  • ResNet-101
  • 같은 backbone RetinaNet 성능 능가
  • DLA-34
    • 속도와 정확도의 가장 좋은 trade-off 제공


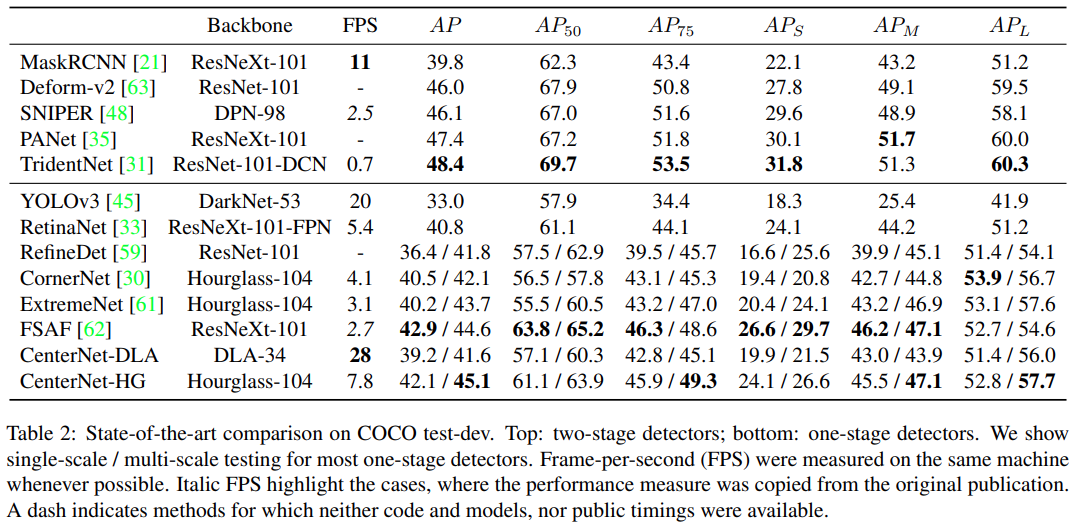
Screenshot from 2024-05-27 22-45-52

  • 2 stage 방법들이 정확도가 더 좋으나, 속도가 느림
  • CenterNet과 sliding window detector 방식의 차이가 없음


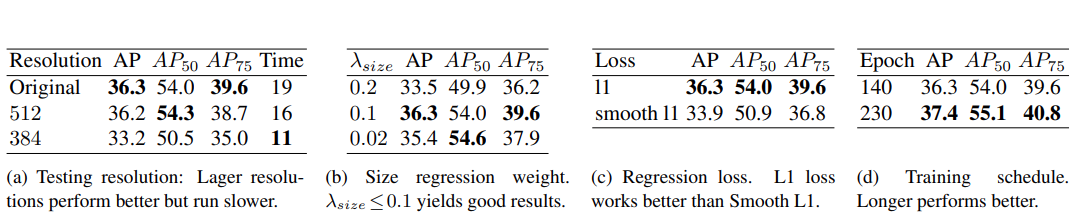
Screenshot from 2024-05-27 22-50-11



Conclusion

CenterNet은 keypoint estimation 방법을 통해 성공적으로 object detection을 한 방법

이 알고리즘은 간단하고, 빠르고 정확하며 NMS post-processing 없이 end-to-end로 미분 가능

2차원 object detection 뿐만이 아니라 다른 task에도 확장 가능

참고