사영 기하학과 동차좌표계
참고
- NVIDIA Jetson Nano와 함께하는 SLAM의 이해와 구현-사영기하학
- 다중관점기하학(Multiple View Geometry in Computer Vision) 책 내용 정리 Part 1 - 사영기하학
사영 기하학 (Projective Geometry)
우리는 유클리디안 기하학(Euclidean geometry)을 사용하여 3D 세상을 표현
즉, 우리가 사는 세상은 유클리디안 기하학을 따름
” 20m 앞으로 쭉 직진하다가, 좌회전하여 10m 가면 목적지” 이런 표현도 유클리디안 기하학을 따르는 표현법
이런 표현법으로 우리는 3D 공간을 표현하고 이렇게 표현하는 공간을 유클리디안 공간이라 함
유클리디안 공간 속에서 위치를 표현하기 위해서 우리는 흔히 알고있는 데카르트 좌표계 (Cartesian coordinates) 이용
유클리드 기하학은 점, 선, 면, 수직/수평과 같은 여러 기하학적 성질들에 대해 정의를 내림

유클리디안 기하학의 3D 공간에서는 ‘‘평행한 두 선은 무한의 거리에서 교차” 한다는 정의 존재
즉, 이는 평행한 두 선이 사실상 교차하지 않음을 의미
기차의 선로는 3D 공간 속 기차의 선로는 평행하여 실제로 교차하지 않지만, 위의 사진을 보면 하나의 픽셀에서 교차하고 있음을 확인
이런 현상은 실체 물체의 크기가 동일하더라도 피사체가 카메라에 더 가까울수록 더 크게 나타나는 원근법으로 인해 발생함
정리하자면, 사진은 유클리디안 기하학을 따르지 않음을 알 수 있음
사진은 이미지에 좌표계에 3D 공간을 투영시키는 것이고 기존의 유클리디안 기하학과 다른 기하학이 필요하고 이를 사영기하학(Projective geometry) 이라 함
3D 공간의 물체가 이미지로 투영되면 아래와 같은 정보들이 손실
- 거리 (Depth)
- 비율 (Scale)
- 직교성 (Otrhogonality)
- 평행성 (Parallelism)
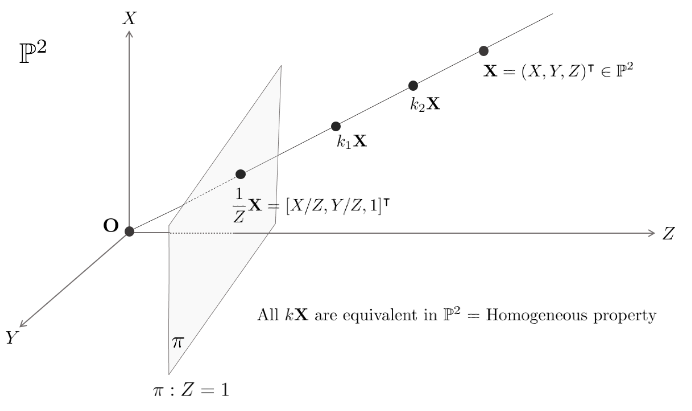
3D 공간 속의 \(\textbf{X}=(X,Y,Z)^{T}\)은 위의 그림 처럼 원점(또는 카메라) 와 연결한 선들의 모든 점이 ${\pi}$ 평면에서 하나의 점에 투영되는 것을 알 수 있음
즉, 실제로 원점, 카메라와의 거리에 상관없이 하나의 점에 투영이 되기 때문에 거리 (Depth) 정보가 사라지는 것을 알 수 있음
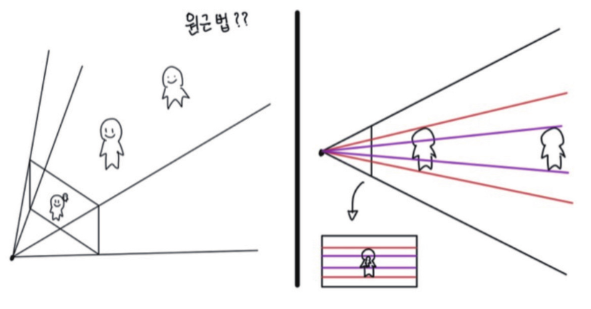
위의 그림을 보면 같은 동일한 사람, 즉 크기가 같은 사람이 있을 때 이 사람과 카메라와의 거리에 따라 이지미지에 투영되는 크기가 달라지는 것을 알 수 있고, 이로 인해 scale 정보가 사라지게 됨
위의 기차 사진 처럼 평행성도 사라지고, 또한 직교성도 사라지게 됨
위에서 확인한 것 처럼 사영 기하학은 유클리드 기하학과는 다른 성질을 가지고 있는 것을 알 수 있음
3D 공간 속 회전을 하는 변환은 유클리드 공간 속에서 유클리드 기하학을 따라 변환을 하기 때문에 유클리드 변환 (Euclidean transformation) 이라고 하며 유클리드 변환은 변환 전과 후의 물체의 길이, 직교성, 평행성, 비율 등이 유지되어야 함
즉, 3D 공간 속에서 물체를 회전시켜도 물체의 길이와 형 태가 그대로 유지되고 물체의 자세만 바뀌는 것
3D 공간의 정보를 2D 이미지에 투영하는 사영 변환(Projective transformation)은 거리, 직교성, 평행성, 비율 정보 모두 유지하지 않아도 됨 유클리드 변환은 사영 변환에 비해 더 많은 전제조건을 가지고 있고 나아가 유클리드 기하학은 사영기하학의 부분집합이라는 것을 알 수 있음
사영 기하학 특징 중 하나는 무한대의 거리의 위치를 포함한 3D 공간에서부터 2D 이미지로 변환하는 과정에 필요 한 모든 위치를 수로 표현할 수 있다는 것
유클리드 기하학에서 평행한 두 개의 직선이 교차하는 지점은 유한의 거리에는 존재하지 않고 무한의 거리에서만 존재하기 때문에 관측할 수 없음
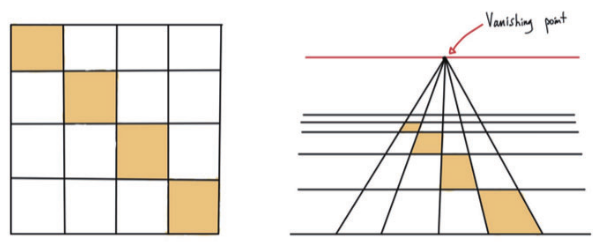
위의 그림과 같이 2D 이미지에 사영 변환했을 때에는 소실점에서 3D에서 평행 선들이 만나는 것을 확인 3D 공간에서의 무한의 거리를 2D 이미지에서는 유한하게 표현할 수 있다는 것을 의미
사영 기하학은 3D 공간에서 2D 이미지로 변환하는 용도로만 사용되는 것이 아닌, 임의의 N+1차원에서 N차원으로의 투영을 통한 차원 축소를 할 때 통용되는 기하학으로 통합 투영을 통한 4차원에서 3차원으로의 투영을 통한 차원 축소, 또 투영을 통한 5차원에 서 4차원으로의 차원 축소도 사영기하학을 통해 표현 가능
동차 좌표계 (Homogeneous coordinates)
유클리드 공간 \(\mathbb{R}^{3}\)에서는 유클리드 기하학을 다룰 때 데카르트 좌표계 $[x\ y\ z]^{T}$ 를 이용
사영 공간 \(\mathbb{P}^{2}\)에서 사영 기하학을 다룰 때는, 동차 좌표계$[x\ y\ z\ w]^{T} $를 사용
동차 좌표계의 정의 중 가장 CV에 잘 맞는 Plucker 정의는 다음과 같은 의미를 가짐
\(X\)라는 객체의 동차좌표계는 0이 아닌 어떠한 스칼라(Scalar) 값을 곱해도 그 좌표 값은 같은 객체를 의미함
즉 유클리디안 기하학의 데카르트 좌표계에서는 아래와 같이 0이 아닌 스칼라 값을 곱해도 같지 않지만
\[\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \neq 2\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\]동차 좌표계에서는 0이 아닌 스칼라 값을 곱해도 같음
\[\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} = 2\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\]유클리디안 공간속 데카르트 좌표계로 표현된 값 $(x, y)$ 를 사영 공간에서 동차좌표계로 표현 할 때는 $(x, y, 1)$ 로 표현
vector의 마지막 값을 scale 이라 하고, 유클리디안 공간 속에서는 1로 표현
위의 좌표에 스칼라 값을 곱하여 ${2x, 2y, 2}$, ${2.5x, 2.5y, 2.5}$, ${10x, 10y, 10}$ 이 되고 이를 다시 비율 값으로 나누면 다시 $(x, y, 1)$로 돌아옴

위의 그림에서 아까 말한 것과 같이 원점과 3차원 공간 상의 \(\textbf{X}\)를 무한하게 연결한 선들의 모든 점은 $\pi$ 평면의 한 점으로 표현이 됨
$\textbf{X}= (1, 2, 3)^{T}$ 이면, 직선 위의 $2\textbf{X}= (2, 4, 6)^{T}$ 은 같은 점으로 투영되므로 2D 사영 공간에서는 같은 값을 가짐
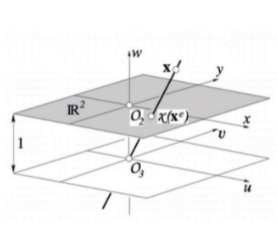
2D 사영 공간을 표현한 것이며, 동차좌표계로 $(u, v, w)$ 로 표현
- $(u, v)$ 는 2차원의 축 방향을 표현한 것이며, $w$는 비율
비율 값이 1로 되어있는 공간이 2D 유클리드 공간 (회색 영역)
유클리드 공간이 사용 공간의 부분 집합임을 알 수 있음