카메라 파라미터
참고
카메라 모델
실제 세상(real world)과 이미지 사이의 관계를 수식으로 근사화 하는 것을 의미
이 관계를 여러 파라미터로 나타낼 수 있는데 이를 카메라 파라미터라고 함
카메라 모델은 카메라 종류에 따라 다르지만 대표적으로 Thin lens model, Pinhole model 가 있음
일반적으로 CV에서는 Pinhole model을 사용
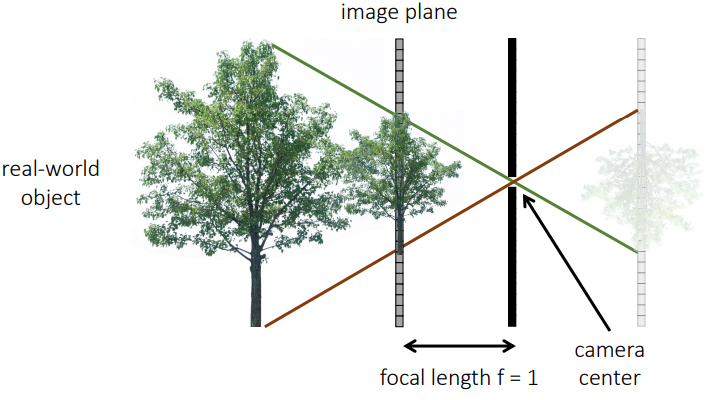
Pinhole 카메라
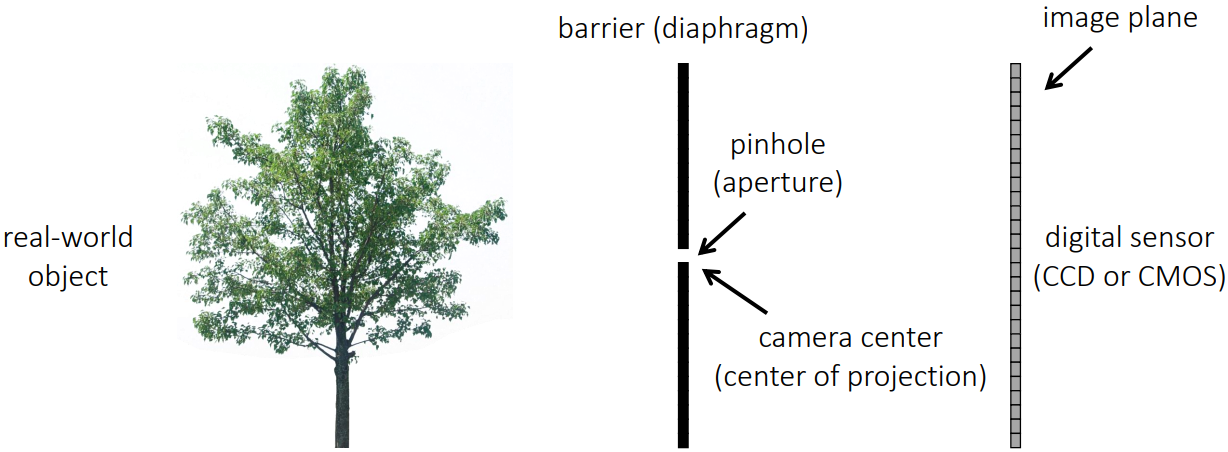
핀홀 카메라는 위의 그림과 같이 aperture라고 부르는 핀홀이 존재하고 이 구멍을 통해 빛이 통과
원점처럼 제약이 걸려있는 위치를 camera center 혹은 center of projection이라 함
핀홀을 통해 통과된 빛은 디지털 센서로 인식이 되어 상이 맺힘
- 필름 등이 될 수도 있음
이 때 상은 아래 그림과 같이 좌우, 상하 반전이 됨
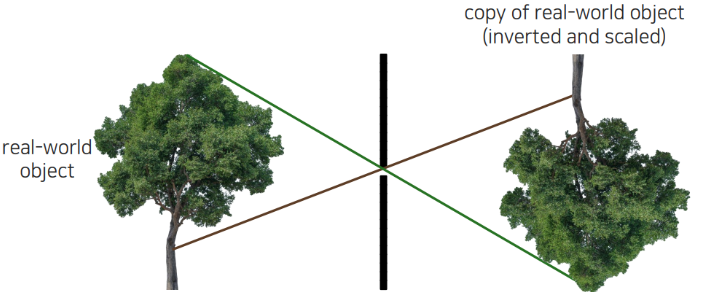
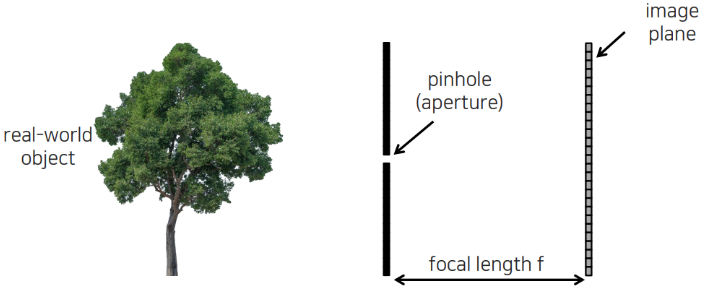
카메라 중심과 image plane 거리를 핀홀 카메라에서는 focal length라고 함
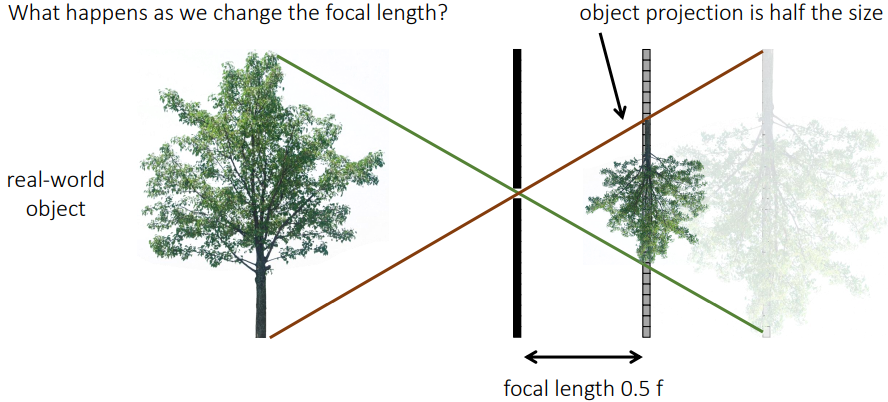
Focal length가 짧아지면, 즉 image plane과 카메라 중심이 가까워지면 아래 그림과 같이 물체가 작은 크기로 상에 맺히게 됨
Pinhole을 기준으로 하여 focal length만큼 앞으로 virtual plane을 만들면 반전이 되지 않은 이미지를 얻을 수 있음
카메라 파라미터
세상 좌표계의 3차원 좌표가 어떻게 2차원 픽셀로 변환되는지 수학적으로 이해하기 위해 필요한 값을 카메라 파라미터라고 함
- \(\textbf{X}\) : 물체에 대한 3차원 좌표 (동차좌표계로 표현)
- $\mathbf{x}$: 카메라 영상 평면에 사영된 2차원 픽셀 좌표계 (동차좌표계로 표현)
- $\text{P}$ : 카메라 파라미터로 구성된 행렬
카메라 파라미터에는 외부 (Extrinsic) 파라미터, 내부 (Intrinsic) 파라미터 2가지가 존재하고 이 두 파라미터를 이용하여 아래와 같은 과정을 거쳐
외부 (Extrinsic) 파라미터
세계 좌표계를 기준으로 상대적인 카메라의 자세를 나타내는 값
다시 말해, 카메라 좌표계와 월드 좌표계 사이의 변환 관계를 설명할 수 있는 파라미터
3D 공간에서 카메라가 어디에 위치해 있고(Translation) 어느 방향을 바라보고 있는지 (Rotation)를 나타냄
회전 변환은 각 축의 회전 변환의 곱으로 표현 할수 있고, 각 축마다 각도를 하나씩 가지므로 3자유도를 가짐
\[R_{x}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\theta_{x}} & -\sin{\theta_{x}}\\ 0 & \sin{\theta_{x}} & \cos{\theta_{x}}\end{bmatrix} \ \ \ \ R_{y}=\begin{bmatrix} \cos{\theta_{y}} & 0 & \sin{\theta_{y}} \\ 0 & 1 & 0\\ -\sin{\theta_{y}} & 0 & \cos{\theta_{y}}\end{bmatrix} \ \ \ \ R_{z}=\begin{bmatrix} \cos{\theta_{z}} & -\sin{\theta_{z}} & 0 \\ \sin{\theta_{z}} & \cos{\theta_{z}} & 0\\ 0 & 0 & 1\end{bmatrix}\]그리고 이 때 각 축으로 이동을 할 수 있기 때문에 3 자유도의 이동 파라미터를 가짐
내부 (Intrinsic) 파라미터
카메라 렌즈와 센서 위치에 의해 결정되어지는 파라미터
초점 거리 (focal length)
핀홀 카메라의 경우 핀홀 (렌즈의 중심)에서 이미지 센서 (CCD, CMOS) 까지의 거리를 의미
카메라에서는 상세 스펙에 실제 물리 단위인 mm 단위로 표현하지만, 카메라 모델에서는 이미지 센서의 cell 크기에 대한 상대적인 pixel 단위로 표현
Image plane의 pixel은 이미지 센서의 cell에 대응되기 때문에 초점 거리가 픽셀 단위라는 의미는 초점 거리가 이미지 센서의 셀 크기에 상대적인 값으로 표현된다는 의미
예를 들어,
카메라 모델에서 초점 거리를 하나의 값 $f$가 아닌 $f_{x}$, $f_{y}$로 나타내는데 이미지 센서의 물리적인 셀 간격이 가로 방향, 세로 방향이 서로 다를 수 있음을 모델링
image plane의 픽셀의 크기가 정사각형이 아니라 width와 height가 다른 경우 다음과 같이 pixel 단위로 표현 가능
\[f_{x} \propto \frac{f \text{ (mm)}}{\text{sensor cell width (mm)}}\times \text{img width (pixel)}\\ f_{y} \propto \frac{f \text{ (mm)}}{\text{sensor cell height (mm)}}\times \text{img height (pixel)}\]예를 들어 100x100 cell size (0.1mm)이고 100x100 의 이미지 해상도를 가진다면 1x1 sensor의 cell이 하나의 pixel을 표현함
0.1mm x f (pixel) = f(mm)
다른 조건이 다 같고 50 x 50의 이미지 해상도를 가지면 2x2 sensor cell이 하나의 pixel 표현
0.2mm x f (pixel) = f(mm)
물리적인 초점 거리는 동일하기 때문에 pixel 단위의 초점 거리는 절반으로 줄어듬
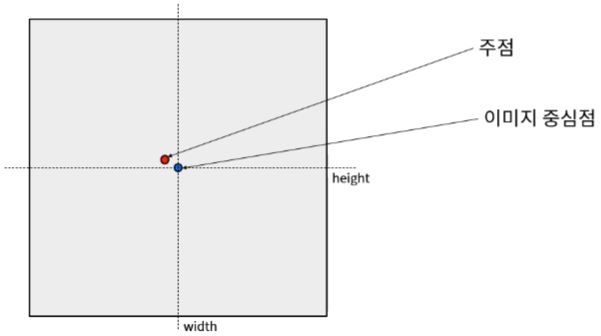
주점 (Principal point)
카메라의 중심, 즉 핀홀에서 image plane에 내린 수선의 발의 영상 좌표이며 Pixel 단위를 사용함
이상적인 경우라면 image plane의 중심점과 주점이 같아야 함
\[c_{x} = \frac{\text{img width}}{2} \\ c_{y} = \frac{\text{img height}}{2}\]하지만 카메라를 만드는 과정 중에 오차가 발생하여 렌즈와 이미지 센서의 수평이 어긋나면 아래와 같이 같은 값을 가지지 못함
비대칭 계수 (Skew coefficient)
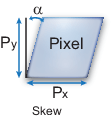
이미지 센서의 cell array의 y축이 기울어진 정도를 나타내고 $\tan\alpha$로 계산
$x$값이 위의 $y\tan\alpha$ 만큼 밀림
요즘 카메라들은 이러한 에러가 거의 없기 때문에 많이 고려하지 않음
렌즈 왜곡 계수 (Distortion coefficient)
렌즈 왜곡계수는 렌즈의 가하학적인 변형을 표현하는 모델에 정의된 파라미터
실제로 핀홀 카메라는 핀홀이 아린 렌즈를 이용하여 빛을 한점(초점) 으로 모음
그렇기 때문에 렌즈에 의한 기하학적 왜곡을 반영해야함
아래 그림은 방사형 왜곡을 나타냄

광선이 광학적 중심에서보다 렌즈의 가장자리에서 더 많이 휘기 때문에 발생함
중심에서 멀어질수록 왜곡의 정도가 심해짐
이를 표현하기 위해 방사 왜곡 계수를 사용
방사형 왜곡 계수는 보통 $k_{1}$, $k_{2}$, $k_{3}$ 으로 나타내고 왜곡이 심하면 $k_{4}$와 같은 추가적인 계수를 이용할 수 있음
이 뿐만 아니라 카메라를 제조하는 과정 중 만들어지는 접선 왜곡 존재
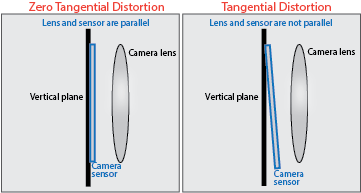
렌즈와 이미지 센서와의 수평이 맞지 않는 경우에 발생함
이를 표현하기 위해 접선 왜곡 계수를 사용
접선 왜곡 계수는 보통 $p_{1}$, $p_{2}$로 나타냄
렌즈가 만들어내는 기하학적 왜곡은 렌즈의 형상과 굴절률과 같은 재료의 광학적 특성에 영향을 받고, 이런 복잡한 물리적 현상을 효과적으로 표현하는 모델은 존재하지 않으며, 대신 간단한 수식으로 근사한 모델을 사용
가장 널리 사용되는 것은 렌즈의 기하학적 왜곡을 다하식으로 근사하는 다항식 왜곡 모델
자세한 내용은 아래 변환 과정에서 설명
변환
세계 좌표계 -> 카메라 좌표계
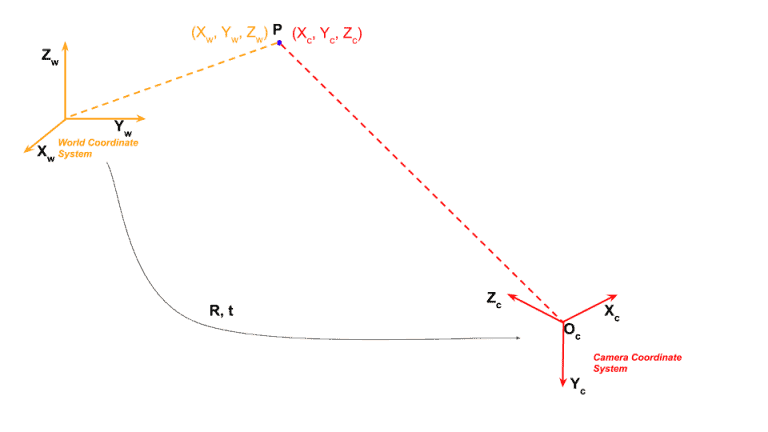
세계 좌표계에 존재하는 점 $\mathbf{P_{W}}$를 \([X_{w}, Y_{w},Z_{w}]^{T}\) 라고 정의하고 세계 좌표계에서의 카메라의 중심 좌표를 \(\mathbf{P}_{O_{c}}=[X_{O_{c}}, Y_{O_{c}},Z_{O_{c}}]^{T}\) 라고 가정
이 때, 세계 좌표계에 있는 점 $\mathbf{P_{W}}$를 카메라 좌표계를 기준으로 변환을 해주어야 하는데 이를 위해서는 세계 좌표계 대비 카메라가 얼마나 rotation 되어있고 translation 되어있는지 알아야 함
$\mathbf{P_{W}}$의 좌표에서 카메라의 \(\mathbf{P}_{O_{c}}\) 의 중심 좌표를 빼는 이동을 거쳐($t$), 카메라의 회전 행렬 $R$을 곱하면 카메라 좌표계에서 바라본 좌표를 구할 수 있음
이를 동차 좌표계로 표현하면 아래와 같음
\[\begin{align*} \begin{bmatrix} \mathbf{P}_{C} \\ 1 \end{bmatrix}&=\begin{bmatrix} R & 0 \\ 0^{T} & 1 \end{bmatrix} \begin{bmatrix} I_{3} & -\mathbf{P}_{O_{C}} \\ 0^{T} & 1 \end{bmatrix}\begin{bmatrix} \mathbf{P}_{W} \\ 1 \end{bmatrix} \\ &=\begin{bmatrix} R & -R\mathbf{P}_{O_{C}} \\ 0^{T} & 1 \end{bmatrix}\begin{bmatrix} \mathbf{P}_{W} \\ 1 \end{bmatrix} \end{align*}\]센서의 image plane에 사영
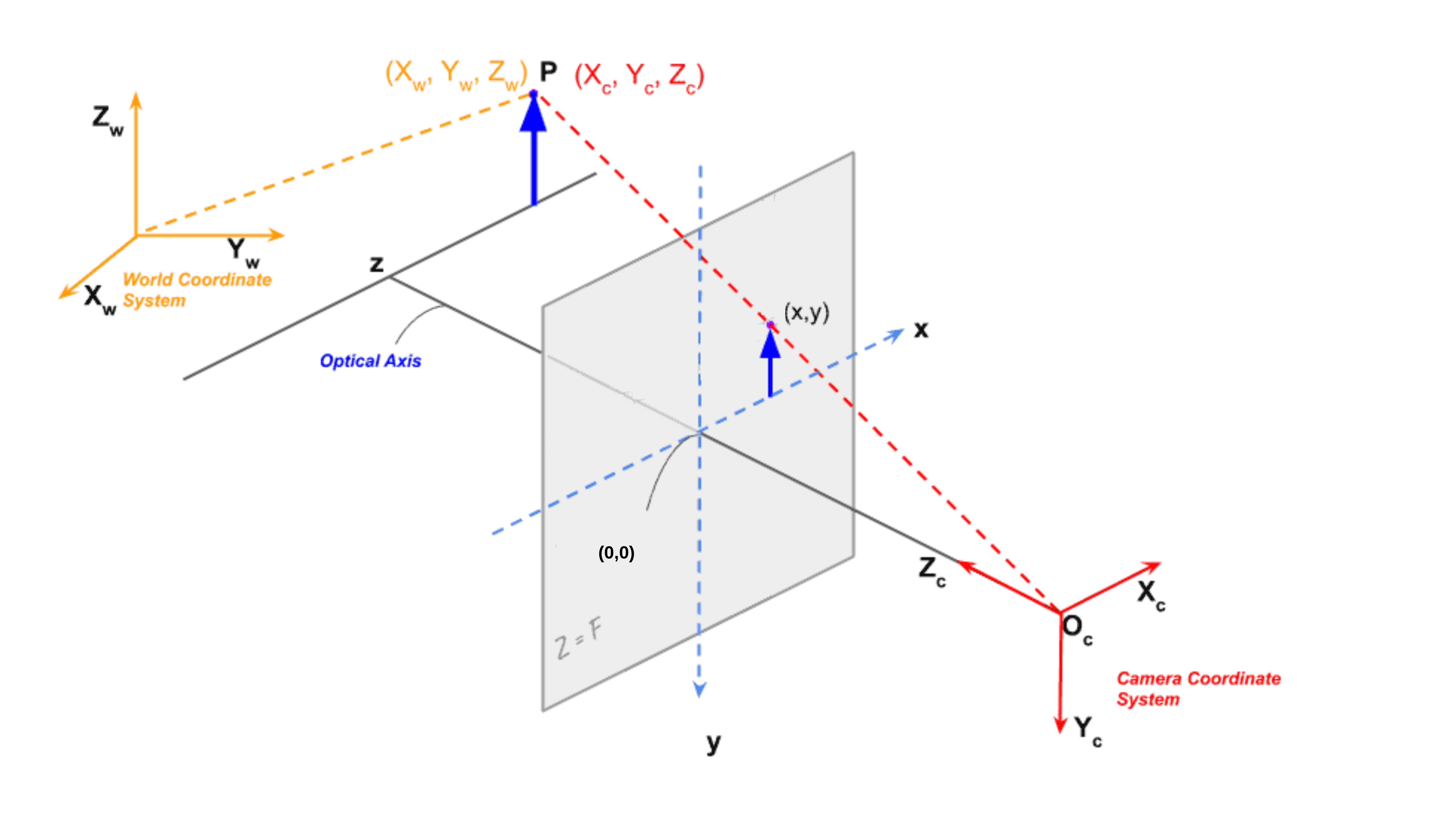
핀홀 카메라 모델에서 왜곡이 없는 렌즈를 사용하고 있다고 가정하고, 점 $P_{c}$가 sensor image plane에 사영되면 위의 그림과 같이 2차원 픽셀값 $(x, y)$를 가지게 됨
센서의 image plane은 사실상 렌즈, 핀홀 뒤에 있지만 기하학적 연산을 편하게 표현하기 위해 렌즈 앞에 위치시키는 것이 일반적
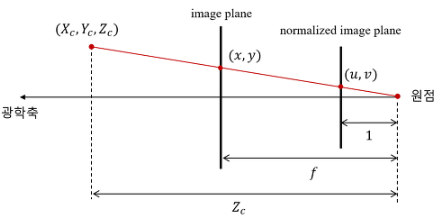
위의 그림 처럼 비례식을 이용하면 값을 쉽게 구할 수 있음
\[X_{C}:Z_{C} =x:f_{x} \ \ \ \ \rightarrow \ \ \ \ x=f_{x}\frac{X_{C}}{Z_{C}} \\ Y_{C}:Z_{C} =y:f_{y} \ \ \ \ \rightarrow \ \ \ \ y=f_{y}\frac{Y_{C}}{Z_{C}}\]위와 같이 유도된 점의 값을 동차 좌표계를 이용하여 표현하면 아래와 같은 행렬의 수식과 같음
\[\begin{align*} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} &=\begin{bmatrix} f_{x} & 0 &0 & 0 \\ 0& f_{y}& 0 & 0\\0&0& 1& 0\end{bmatrix} \begin{bmatrix} X_{C} \\Y_{C} \\ Z_{C} \\ 1 \end{bmatrix}\\ &=\begin{bmatrix} f_{x}X_{C} \\ f_{y}Y_{C} \\ Z_{C} \end{bmatrix}=\begin{bmatrix} f_{x}\frac{X_{C}}{Z_{C}} \\ f_{y}\frac{Y_{C}}{Z_{C}} \\ 1 \end{bmatrix} \end{align*}\]픽셀 좌표계로 변환
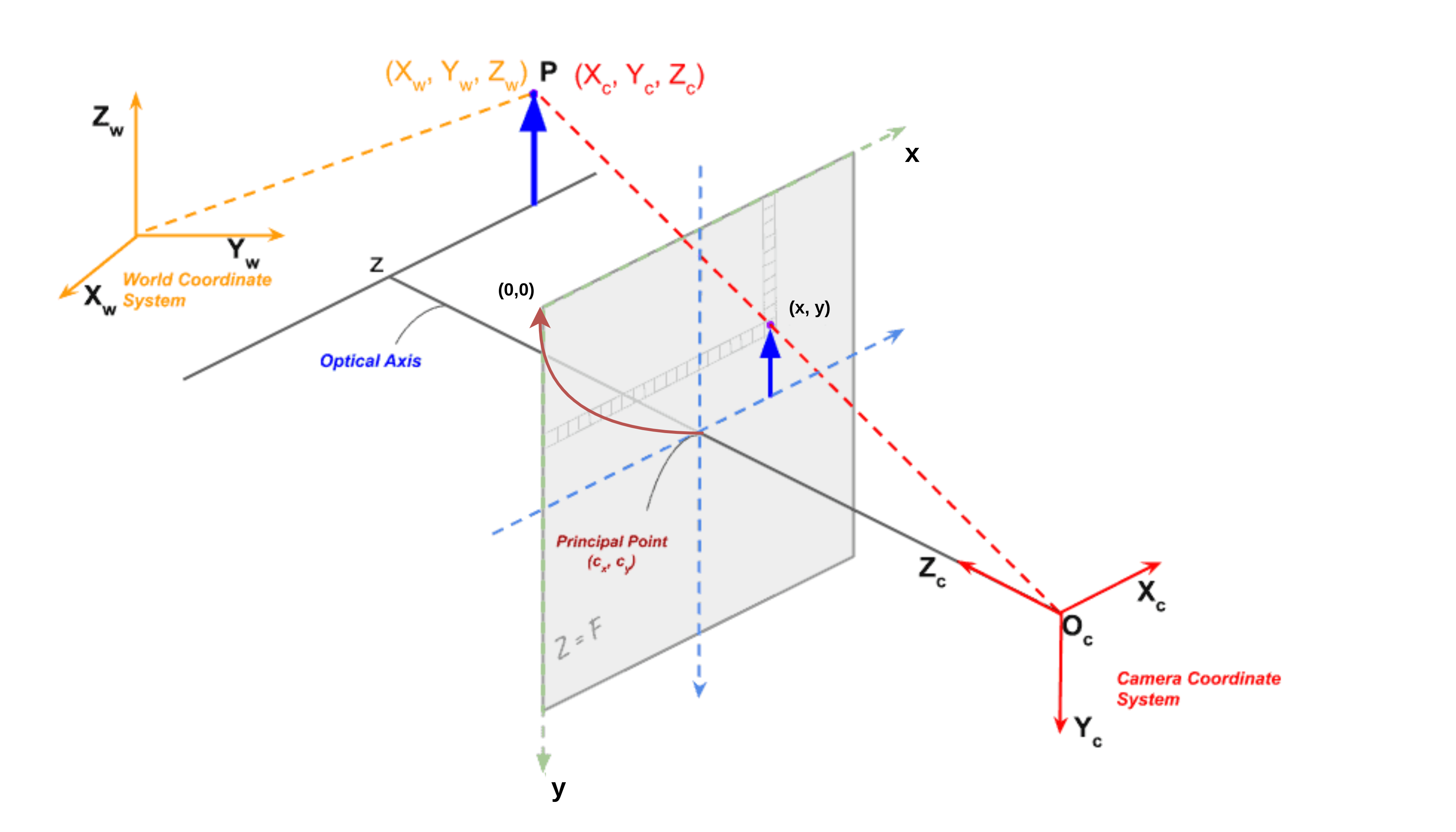
앞에서 사영시켜서 구한 pixel 좌표는 센서의 image plane과 optical axis가 겹치는 부분이 원점을 가짐
하지만 실제 이미지 좌표계는 좌상단이 원점이 되기 때문에 주점을 더하여 수정
\(x = x+c_{x}\\ y = y+c_{z}\) 이를 동차좌표계로 표현하면 아래와 같은 행렬을 얻을 수 있음
\[\begin{align*} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} &=\begin{bmatrix} 1 &0&c_{x} \\ 0 &1&c_{y}\\0&0&1\end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \end{align*}\]이 때 만약 skew가 존재한다면 x 값이 변화가 존재하기 때문에 이를 반영해주는 파라미터 $s$를 추가
\[\begin{align*} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} &=\begin{bmatrix} 1 &s&c_{x} \\ 0 &1&c_{y}\\0&0&1\end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \end{align*}\]일반적으로 카메라의 왜곡이 존재하지 않는다고 가정하면 아래의 행렬이 카메라 캘리브레이션 행렬 $K$라고 할 수 있음
\[K= \begin{bmatrix} f_{x} &s&c_{x} \\ 0 &f_{y}&c_{y}\\0&0&1\end{bmatrix}\]앞에서 표현한 모든 과정을 거치면 아래와 같이 표현 가능
렌즈 왜곡 변환
위의 과정은 렌즈의 왜곡이 없는 경우를 표현
하지만 실제로 렌즈의 왜곡이 발생되기 때문에 이를 고려해야 함
왜곡의 수학적 모델의 표현은 카메라 내부 파라미터의 영향이 제거된 normalized image plane에서 정의
이 때의 좌표를 $[x_{u}, y_{u}, 1]^{T}$라고 표현
- $u$는 undistorted를 의미함
이때 왜곡된 좌표를 $[x_{d}, y_{d}, 1]^{T}$ 라 하면 왜곡 모델은 다음과 같이 나타낼 수 있음
\[\begin{align*} \begin{bmatrix} x_{d} \\ y_{d}\end{bmatrix} = \overbrace{(l+k_{1}r_u^{2}+k_{2}r_{u}^{4}+k_{3}r_{u}^{6})}^{\text{방사형 왜곡}} \begin{bmatrix} x_u \\ y_{u} \end{bmatrix}+ \overbrace{\begin{bmatrix} 2p_{1}x_{u}y_{u}+p_{2}(r^{2}_{u}+2x^{2}_{u}) \\ 2p_{2}x_{u}y_{u}+p_{1}(r^{2}_{u}+2y^{2}_{u})\end{bmatrix}}^{\text{접선 왜곡}} \end{align*}\]- 이 때, \(r^{2}_{u}={x}_{u}^{2}+ y_{u}^{2}\)