참고

  1. NVIDIA Jetson Nano와 함께하는 SLAM의 이해와 구현
  2. Coordinate Transformations & Representations for Rotations
  3. 6. 회전의 수학 II : 사원수
  4. 축각 회전 (Axis-Angle Rotation) 또는 로드리게스 회전 (Rodrigues Rotation)



3D 변환

Computer vision 에서는 Euclidean transformation, 즉 rigid transformation에만 관심이 있음

rigid transformation을 적용해도 물체의 형태는 변하지 않고 회전, 이동 변환만 함



회전 표현법

Euler Angle

3차원 공간상의 어떤 물체에 대한 회전 표현하기 위해 고정된 3차원의 직교 좌표계 사용하는 방법

이 때 각각의 고정된 축에 대해서 Roll, Pitch, Yaw 라는 3개의 파라미터로 회전을 표현 표현

각 축의 회전은 오른손 법칙을 따르기 때문에 반시계 방향이 +

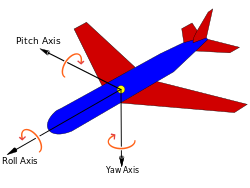
Yaw_Axis_Corrected.svg

출처


각각 $x$축, $y$축, $z$축 에 대한 오일러각 $\alpha$, $\beta$, $\gamma$를 이용하여 회전 행렬을 얻으면 다음과 같이 표현 가능


\[R_{1}(\alpha)=\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\alpha} & -\sin{\alpha}\\ 0 & \sin{\alpha} & \cos{\alpha}\end{bmatrix} \ \ \ \ R_{2}(\beta)=\begin{bmatrix} \cos{\beta} & 0 & \sin{\beta} \\ 0 & 1 & 0\\ -\sin{\beta} & 0 & \cos{\beta}\end{bmatrix} \ \ \ \ R_{3}(\gamma)=\begin{bmatrix} \cos{\gamma} & -\sin{\gamma} & 0 \\ \sin{\gamma} & \cos{\gamma} & 0\\ 0 & 0 & 1\end{bmatrix}\]

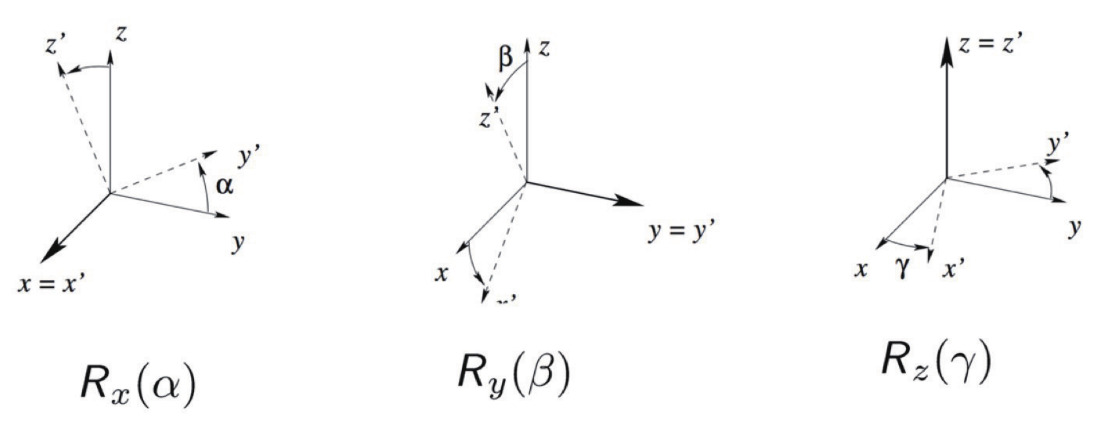
Screenshot from 2024-06-29 10-54-58


이렇게 얻어진 각각의 고정된 축에 대한 회전 행렬을 행렬 곱셈을 통해 하나로 합치면 3차원 강체 (Rigid-body)에 대한 임의의 회전 표현 가능

행렬 곱셈은 교환 법치기 성립하지 않기 때문에 축을 아래와 같이 어떤 순서로 하는지에 따라서 회전의 결과가 바뀌는 것을 주의

  • 뒤의 행렬부터 계산


\[R_{A}=(\alpha, \beta, \gamma)=R_{3}(\gamma)R_2(\beta)R_{1}(\alpha) \\ \\ \begin{bmatrix} \cos\gamma \cos\beta & -\sin\gamma \cos\alpha +\cos\gamma\sin\beta\sin\alpha& \sin\gamma\sin\alpha+\cos\gamma\sin\beta\cos\alpha \\ \sin\gamma\cos\beta & \cos\gamma\cos\alpha+\sin\gamma\sin\beta\sin\alpha & -\cos\gamma\sin\alpha+\sin\gamma\sin\beta\cos\alpha \\ -\sin\beta & \cos\beta\sin\alpha & \cos\beta\cos\alpha \end{bmatrix}\]


\[R_{B}=(\alpha, \beta, \gamma)=R_{1}(\alpha)R_2(\beta)R_{3}(\gamma) \\ \\ \begin{bmatrix} \cos\gamma\cos\beta & -\sin\gamma \cos\beta& \sin\beta \\ \cos\gamma\sin\beta\sin\alpha+\sin\gamma\cos\alpha & -\sin\gamma\sin\beta\sin\alpha+\cos\gamma\cos\alpha & -\cos\beta\sin\alpha\\ -\cos\gamma\sin\beta\cos\alpha+\sin\gamma\sin\alpha & \sin\gamma\sin\beta\cos\alpha+\cos\gamma\sin\alpha & \cos\beta\cos\alpha \end{bmatrix}\]


반대로 회전 행렬 $R$이 주어졌을 때 오일러 각으로 변환하는 것도 가능

$R_{A}$를 예를 들어 설명하면 다음과 같음

첫번째 column이 가장 간단하기 때문에 이를 기준으로 설명


\[\begin{bmatrix} \cos\gamma \cos\beta \\ \sin\gamma\cos\beta \\ -\sin\beta \end{bmatrix} =\begin{bmatrix} r_{11} \\ r_{21} \\ r_{31} \end{bmatrix}\] \[\begin{align*} r_{11}^{2}+r_{21}^{2}&=\cos\gamma^{2} \cos\beta^{2}+\sin\gamma^{2}\cos\beta^{2}\\ &=(\cos\gamma^{2}+\sin\gamma^{2})\cos\beta^{2}= \cos\beta^{2} \end{align*}\]


$\beta$에 대한 $\sin$, $\cos$ 을 $r_{11}$, $r_{21}$, $r_{31}$ 로 표현 가능


\[\cos\beta= \pm \sqrt{r_{11}^{2}+r_{21}^{2}} \\ \sin\beta=-r_{31}\]


\[\tan\beta=\frac{\sin\beta}{\cos\beta}=\frac{-r_{31}}{\pm \sqrt{r_{11}^{2}+r_{21}^{2}}}\\ \beta=\tan^{-1}\frac{-r_{31}}{\pm \sqrt{r_{11}^{2}+r_{21}^{2}}}\]


이 때 분모에 따라서 경우를 나누어 생각해 볼 수 있음


$\pm \sqrt{r_{11}^{2}+r_{21}^{2}} !=0 $ 일 때,

$\pm \sqrt{r_{11}^{2}+r_{21}^{2}} > 0$ 이면 (즉, $\cos\beta > 0$) 제 1, 4분면에 위치하기 때문에 $-90^{\circ} <\beta < 90^{\circ}$ 범위에 존재

$\pm \sqrt{r_{11}^{2}+r_{21}^{2}} < 0$ 이면 ($\cos\beta < 0$) ,

$r_{31} < 0$ , 제 2 사분면에 위치하기 때문에 $90^{\circ} <\beta < 180^{\circ}$

$r_{31} > 0$, 제 3 사분면에 위치하기 때문에 $-180^{\circ} <\beta < -90^{\circ}$

이 경우에만 회전 행렬로 오일러 각 구하는 것이 가능


$\pm \sqrt{r_{11}^{2}+r_{21}^{2}}=0$ 인 경우 ($\cos\beta=0$)

$\beta=90^{\circ}$ 이거나 $\beta=-90^{\circ}$의 값을 가지는데,

$\beta=90^{\circ}$ 인 경우

\[\begin{bmatrix} 0 & -\sin\gamma \cos\alpha +\cos\gamma\sin\alpha& \sin\gamma\sin\alpha+\cos\gamma\cos\alpha \\ 0 & \cos\gamma\cos\alpha+\sin\gamma\sin\alpha & -\cos\gamma\sin\alpha+\sin\gamma\cos\alpha \\ -1 & 0 & 0 \end{bmatrix} \\ \begin{bmatrix} 0 & -\sin(\gamma-\alpha) & \cos(\gamma-\alpha) \\ 0 & \cos(\gamma-\alpha) & \sin(\gamma-\alpha) \\ -1 & 0 & 0 \end{bmatrix}\]

이 때, Gimbal Lock 현상이 발생함

Gimbal Lock 현상이란 각 축에 대한 회전을 진행하다 두 개의 축이 겹치게 되어서 회전각이 소실되는 현상

자유도가 줄어들기 때문에 표현력이 떨어짐


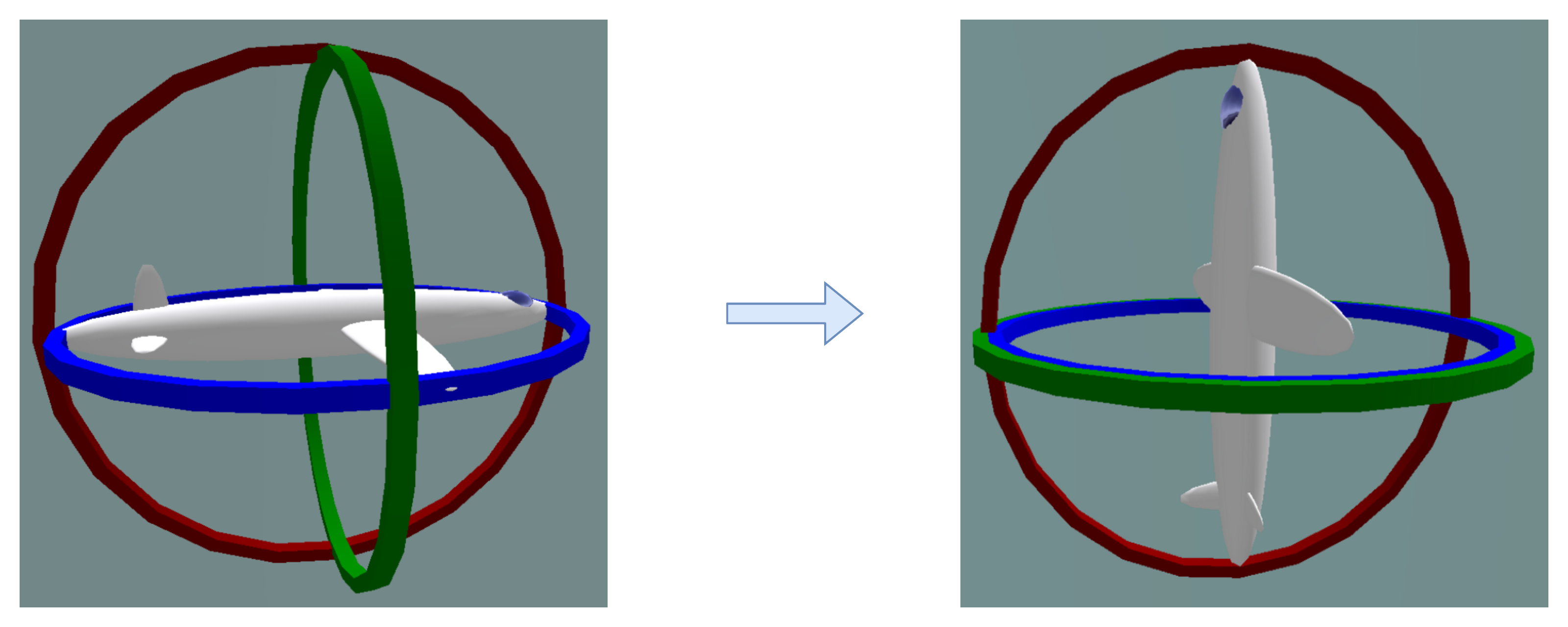
gimbal_rock


Gimbal Lock

  • 자유도 하나가 사라져버려서 표현력이 떨어져버림

SO(3)

Special Orthogonal Matrix (3D) \(SO(3)=\{R\in \mathbb{R}^{3\times 3}|R^{T}R=I, \text{det}(R)=1\}\)

\[R_{x}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{(\theta_{x})} & -\sin{(\theta_{x})}\\ 0 & \sin{(\theta_{x})} & \cos{(\theta_{x})}\end{bmatrix}\] \[R_{y}=\begin{bmatrix} \cos{(\theta_{y})} & 0 & \sin{(\theta_{y})} \\ 0 & 1 & 0\\ -\sin{(\theta_{y})} & 0 & \cos{(\theta_{y})}\end{bmatrix}\] \[R_{z}=\begin{bmatrix} \cos{(\theta_{z})} & -\sin{(\theta_{z})} & 0 \\ \sin{(\theta_{z})} & \cos{(\theta_{z})} & 0\\ 0 & 0 & 1\end{bmatrix}\]

Quanternion (사원수)

3개의 허수(Complex number)와 하나의 실수 (Real Number)를 이용하여 회전을 표현하는 방법 \(\hat{q}=d+a\mathbf{i}+b\mathbf{j}+c\mathbf{k}=(d, (a,b, c))\)

Axis-Angle

3차원 공간에서 임의의 회전 축 하나를 벡터$\bar{n}$로 표현하고, 이 축에 대한 회전각 $\theta$를 이용해 회전을 표현하는 방법

로드리게스 회전이라고 하기도 함

(축각 방식 중 하나인지, 같은 말인지… )


로드리게스 회전의 공식은 아래은 순서로 유도할 수 있음

5

출처


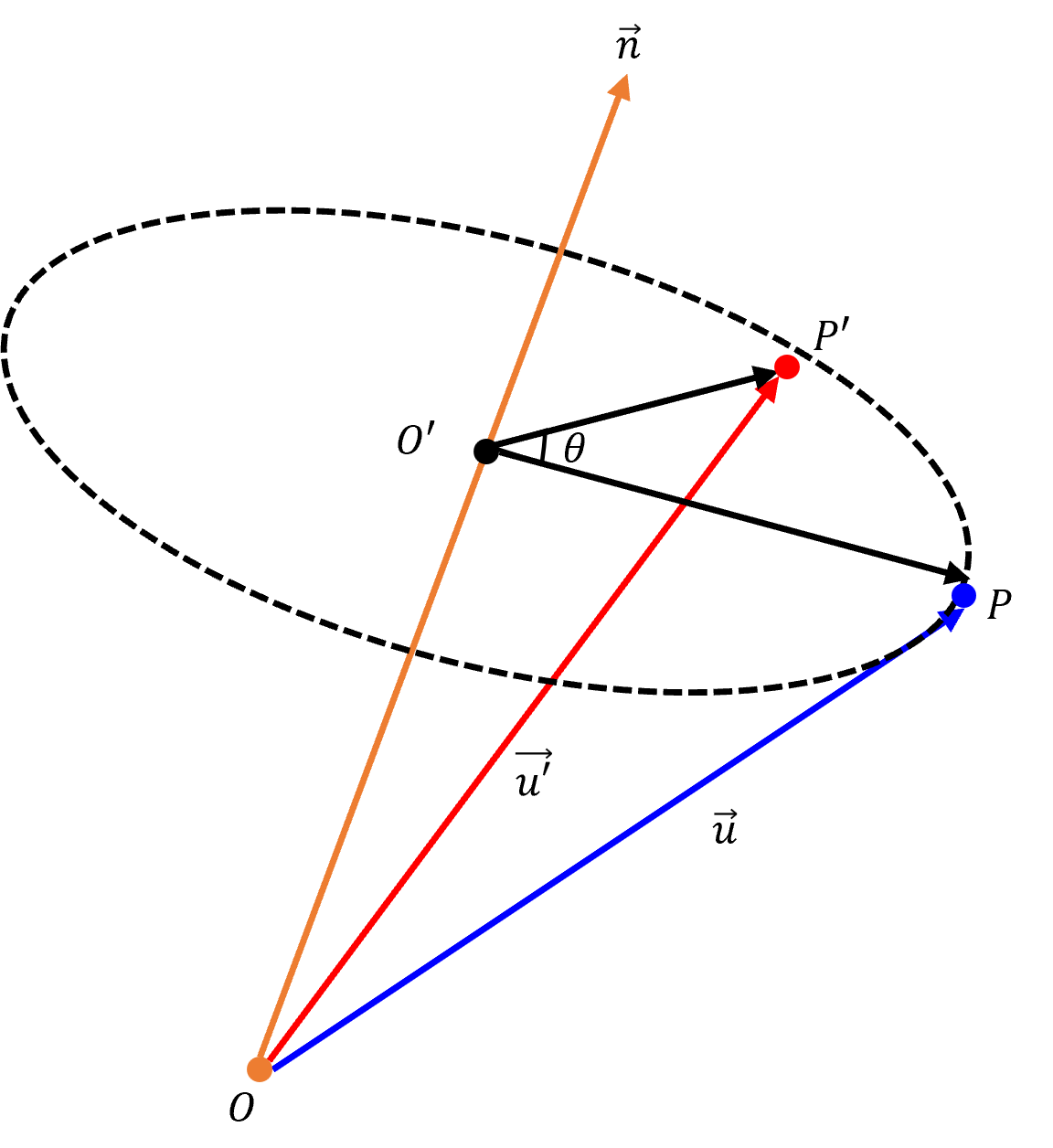
가장 먼저 원점 $O$에서 $O^{‘}$을 향하는 vector를 $v$라고 하고 이를 계산

\[\vec{v}=(\vec{u}\cdot\vec{n})\vec{n}\]
  • 벡터 내적을 이용하여 투영


위에 구한 값을 이용하여 \(\overrightarrow{O^{'}P}\) 계산

\[\overrightarrow{O^{'}P}=\vec{u}-\vec{v}\]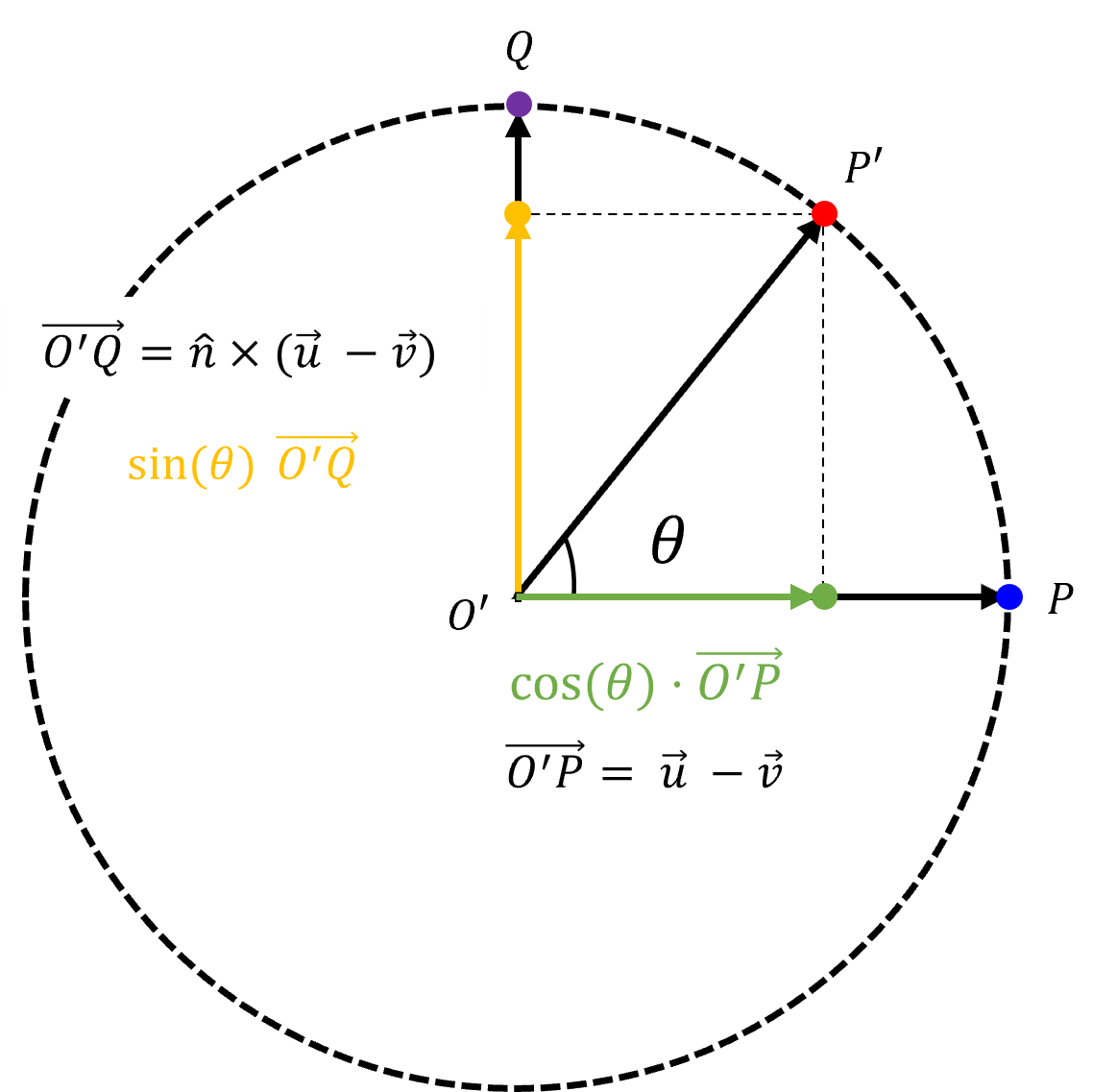


7

출처


\(\overrightarrow{O^{'}P^{'}}\)의 \(\overrightarrow{O^{'}P}\) 방향으로의 vector 는

\[\cos\theta\ \overrightarrow{O^{'}P}\]


\(\overrightarrow{O^{'}P}\)와 수직인 vector인 \(\overrightarrow{O^{'}Q}\) 계산

\[\overrightarrow{O^{'}Q}= \vec{n} \times (\vec{u} - \vec{v})\]
  • \(\overrightarrow{O^{'}P}\), $ \vec{n}$ 두 벡터와 모두 수직인 벡터이기 때문에 외적을 사용하여 계산 가능


\(\overrightarrow{O^{'}P^{'}}\)의 \(\overrightarrow{O^{'}Q}\) 방향으로의 vector는

\[\sin{\theta}\ \overrightarrow{O'Q}\]


두 벡터의 합으로 \(\overrightarrow{O'P'}\) 계산

\[\begin{align*} \overrightarrow{O'P'} &= \cos{\theta} \ \overrightarrow{O'P} + \sin{\theta}\ \overrightarrow{O'Q} \\ &= \cos{\theta} (\vec{u} - \vec{v}) + \sin{\theta} (\bar{n} \times (\vec{u} - \vec{v})) \\ &= \cos{(\theta)} (\vec{u} - \vec{v}) + \sin{\theta} (\hat{n} \times \vec{u} - \bar{n} \times \vec{v}) \\ &= \cos{\theta} (\vec{u} - \vec{v}) + \sin{\theta} (\bar{n} \times \vec{u}) \end{align*}\]


지금까지 구한 값을 이용하여 \(\overrightarrow{OP'}\) 아래와 같은 식으로 구할 수 있음

\[\begin{align*} \overrightarrow{OP'} &= \vec{v} + \cos{\theta} (\vec{u} - \vec{v}) + \sin{\theta} (\bar{n} \times \vec{u})\\ &=\bar{u}\cdot \bar{n}+\cos{\theta} (\vec{u} - \bar{u}\cdot \bar{n}) + \sin{\theta} (\bar{n} \times \vec{u}) \end{align*}\]
  • 내적과 외적으로 계산 가능



Quanternion (사원수)

3개의 허수(Complex number)와 하나의 실수 (Real Number)를 이용하여 회전을 표현하는 방법 \(\hat{q}=d+a\mathbf{i}+b\mathbf{j}+c\mathbf{k}=(d, (a,b, c))\)

카테고리:

업데이트:

참고