Graph

이미지와 문장과 같은 Data Representation 방법 중 하나

Graph Structure

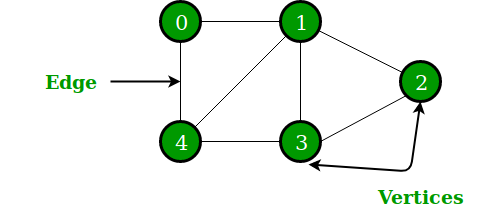
graph

출처

Vertex (Node) 와 Edge로 구성

Graph에는 edge에 방향이 존재하는 경우도 있고, 중요도를 나타내는 그래프도 존재


Graph Representation

GCN을 사용하기 위해 그래프의 노드 정보와 연결성은 다음과 같은 방법으로 표현

graph_representation

  1. Adjacent matrix A
    • Node 간 connectivity 의미
  2. Node feature matrix
    • 각 node에 담긴 특징, 정보를 의미



Graph Convolution Network

CNN 특징

Convolution layer은 kernel의 Weight Sharing 을 통해 파라미터 수를 줄여 계산의 효울과 overfitting을 막음

Local의 feature를 학습이 가능하며 MLP에 비해 이미지에 변화에 예민하지 않음


CNN은 각 layer를 통과하면서 activation map의 값을 업데이트함

Activation map의 값은 이미지의 특성, 상태 정보를 나타냄


그래프의 경우에는 그래프 자체의 형태는 바꾸지 않으면서 각 노드가 가지고 있는 정보를 학습

즉, Graph Convolution layer를 거치면서 node feature maxtrix의 값을 update 하며 값을

GCN

134

출처

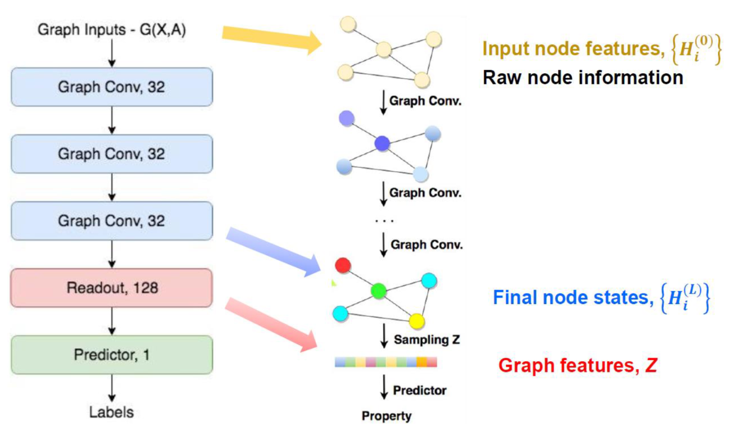
일반적인 Graph Convolution Network는 3개의 layer를 가짐

Graph Convolution layer

기본적인 GCN parameter update 과정

GCN에서 학습하며 파라미터를 없데이트 할 때 CNN의 특성을 고려하여 weight sharing 을 해야한다는 점과 local feature를 추출해야 한다는 점을 고려하여 적용해야 함


아래와 같은 노드가 존재할 때 1번 노드에 대한 정보를 업데이트 하는 과정


1번 노드에 연결된 노드에 대한 feature에 공유하는 weight를 곱하여 더하는 과정으로 업데이트

node_info


\(H_{1}^{(l+1)}=\sigma({\color{Blue}H_{1}^{(l)}W^{(l)}}+{\color{Yellow}H_{2}^{(l)}W^{(l)}}+{\color{Green}H_{3}^{(l)}W^{(l)}}+{\color{red}H_{4}^{(l)}W^{(l)}}+b^{(l)})\\\)

\[H_{i}^{(l+1)}=\sigma(\sum_{j\in N(i)}H_{j}^{(l)}W^{(l)}+b^{(l)})\]
  • \(W, b\) : 학습해야 하는 파라미터
  • \(H\) : Hidden state를 의미하고 node feature matrix를 의미
  • \(\sigma\) : 활성화 함수


위의 식을 일반화하여 나타내면 아래와 같음

\[H_{i}^{(l+1)}=\sigma(\sum_{j\in N(i)}H_{j}^{(l)}W^{(l)}+b^{(l)})\]


특정 노드와 연결되어있는 노드들의 정보를 주기 위해 Adjacency matrix 추가

\[H^{(l+1)}=\sigma(AH^{(1)}W^{(l)}+b^{(1)})\]
  • \(A\) : Adjancy matrix


위와 같이 계산을 하면 두 가지 문제 발생

  1. 업데이트 할 때 자기 자신 node의 feature 를 반영하지 못함
  2. Gradient vansing, expoiding
    • 다른 노드들과 연결이 많은 노드들은 feature representation에서 큰 값을 가져 exploding gradient 발생
    • 다른 노드들과 연결이 적은 노드들은 feature representation에서 작은 값을 가져 vanishing gradient 발생


자기 자신 node feature를 반영하지 못하는 문제를 해걀하기 위해서

Adjacency matrix $A$ 에 Identity Matrix $I$ 를 더하여 해결

A~


\[H^{(l+1)}=\sigma(\tilde{A}H^{(1)}W^{(l)}+b^{(1)})\\ \tilde{A}=A+I\]


Gradient vanishing, expolding 문제는 정규화를 통해 해결

Degree matrix $D$에 Identity Matrix $I$를 더한 값을 이용하여 정규화

degree


\[H^{(l+1)}=\sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(1)}W^{(l)}+b^{(1)})\\ \tilde{D}=D+I\]


위의 정규화 식은 Semi-supervised classification with graph convolutional networks 논문 참고함


Readout

같은 구조를 같은 그래프여도 Adjacency matrix가 다를 수 있음

대칭, 회전에 의해 행렬 내 순서가 다를 수 있기 때문에 Readout layer를 통해 이를 해결

그래프의 Permutation Invariance를 유지시켜줌

\[z_{G}=\tau(\sum_{i\in G}MLP(H_{i}^{(L)}))\]

위의 과정을 통해서 같은 그래프에 대하여 다른 노드의 순서를 같은 경우에도 동일한 결괄를 낼 수 있음이 수학적으로 증명

이 과정을 통해 앞서 생성된 feature를 그래프 전체를 표현하느 하나의 vector로 나타낼 수 있음

이러한 특징 때문에 전체 그래프에 대한 task를 진행할 때 사용


Fully-connected Layer

일반적으로 CNN에서도 사용하는 FC layer와 같음



참고

  1. https://www.youtube.com/watch?v=YL1jGgcY78U
  2. https://github.com/heartcored98/Standalone-DeepLearning/blob/master/Lec9/Lec9-A.pdf
  3. https://arxiv.org/pdf/1901.00596.pdf
  4. https://littlefoxdiary.tistory.com/16
  5. https://arxiv.org/pdf/1609.02907.pdf



카테고리:

업데이트:

참고