참고

아래 자료를 참고하여 정리

  1. https://www.youtube.com/watch?v=dhzLQfDBx2Q
  2. https://www.youtube.com/watch?v=BiQx5ISVdxU
  3. https://drive.google.com/file/d/1tBHavj2v8GgsdOx4UMIYRN9lGvcDWejQ/view



Point Cloud Registration

Point Cloud Registration은 source point cloud와 target point cloud의 정렬을 하는 변환을 찾는 과정

즉, 정렬을 잘하는 Rotation Matrix $R$ 과 Translation Matrix $t$ 를 찾는 과정

Point cloud에 대해서 어떤 정보를 가지고 있는지에 따라서 해결 방법이 달라짐

  1. Known Data Association
    • 두 Point Cloud 간 대응 관계 (Correspondence) 정보를 아는 경우
  2. Unknown Data Association
    • 두 Point Cloud 간 대응 관계 (Correspondence) 정보를 모르는 경우


Known Data Association

두 Point 간 대응 관계에 대한 정보가 있는 경우에는 Exact한 solution을 찾을 수 있음

SVD를 활용하여 Rotation Matrix와 Translation Matrix를 찾아냄

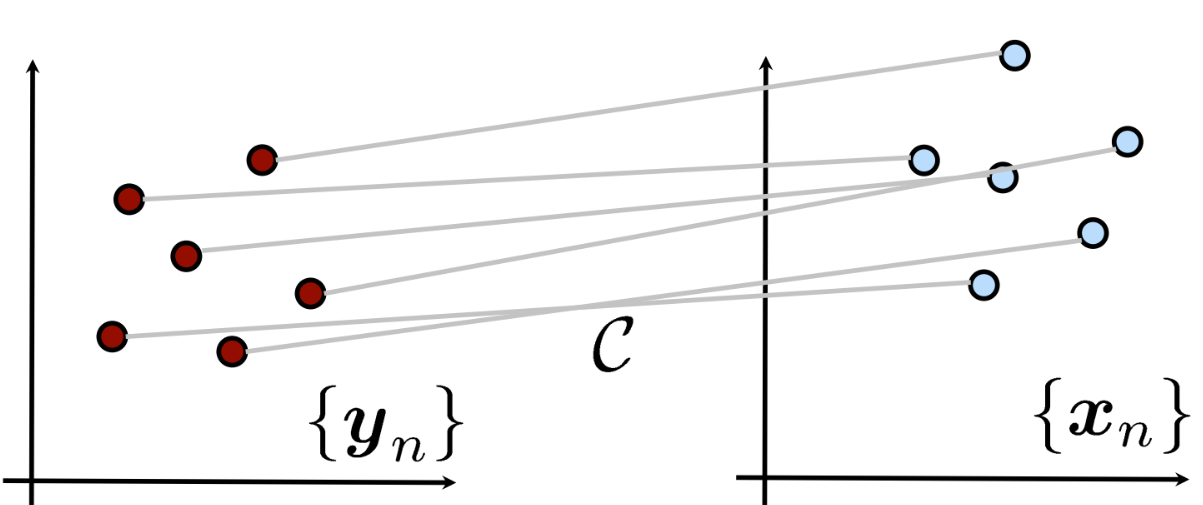
Screenshot from 2024-04-23 01-26-56

출처


Source point cloud를 $x$, target point cloud를 $y$ 라 하면

Source point cloud를 $R$과 $t$을 사용하여 변환한 point cloud는 $\bar{x}_{n}$

\[\bar{x}_{n}=Rx_{n}+t \\\]


변환된 $\bar{x}_{n}$과 target point cloud 의 MSE를 최소화 하는 방법으로 $R$과 $t$를 구함

\[\sum_{(i, j)\in C} ||y_{i}-Rx_{j}-t||^{2} \to min\]


이를 구하기 위해서 point cloud의 질량 중심을 일치시켜야 함

질량 중심을 일치시키기 위해 각 point cloud의 weighted mean 계산 ($x_{0}$, $y_{0}$)

이 때, $p_{n}$은 가중치

\[x_0=\frac{\sum{x_{n}p_{n}}}{\sum{p_{n}}} \\ y_0=\frac{\sum{y_{n}p_{n}}}{\sum{p_{n}}}\]


Weight Sum을 활용하여 cross covariance matrix H 계산

\[H=\sum(x_{n}-x_{0})(y_{n}-y_{0})^{T}p_{n}\]


$H$에 대한 SVD 계산

\[SVD(H)=UDV^{T} \\\]


SVD 값을 이용하여 Rotation Matrix $R$ 계산

\[R=VU^{T}\]


위에서 구한 값들을 이용하여 $t$ 계산 \(t=y_{0}=Rx_{0}\)


Unknown data association

직접적으로 optimal solution을 구할 수 없고 correspondence 정보를 직접 구해 추정해야 함

즉, Rotation Matrix $R$ 과 Translation Matrix $t$ 을 한번에 찾기 어려움

보편적인 방법은 두 포인트 클라우드로부터 correspondence를 추정하고 이를 기반으로 반복적으로 Rotation Matrix $R$ 과 Translation Matrix $t$ 을 수정하여 에러를 최소화 하는 것

대표적인 방법으로 ICP와 Global Registration 존재


ICP (Iterative Closest Point)

가장 기본이 되는 ICP의 알고리즘은 다음과 같음


  1. 두 point cloud $x_{n}$, $y_{n}$의 대략적인 대응 관계의 초기값 설정
    • 보통 하나의 point cloud $x_{n}$의 각 point에서 또 다른 point cloud $y_{n}$의 가장 가까운 거리의 점과 대응 관계 형성
  2. Rotation Matrix $R$ 과 Translation Matrix $t$ 계산
    • SVD 등의 방법 이용
  3. 앞에서 구한 $R$ 과 $t$ 를 이용하여 $\bar{x_{n}}=R\times x_{n}+t$ 을 계산
  4. $\bar{x_{n}}$ 과 $y_{n}$의 차이가 설정한 threshold 값보다 작아질 때 까지 위의 과정 반복


이런 ICP 방법은 경우에 따라 Iteration을 많이 요구할 수도 있고 부정확하게 초기값 설정하는 경우는 수렴이 늦어지거나 잘못된 local minima에 빠질 수 있음

가까운 거리를 기준으로 대응 관계를 정하기 때문에 일반적으로는 point cloud 거리가 가까울수록 ICP가 초기에 잘 적용되고 iteration도 줄일 수 있음


가장 기본이되는 ICP는 가장 가까운 point를 통해 data assosiation을 진행하였지만 그 외에도 다양한 방법을 사용하여 위의 단점들을 극복 가능


요즘에 특히 Point-to-Plane 방식을 많이 사용


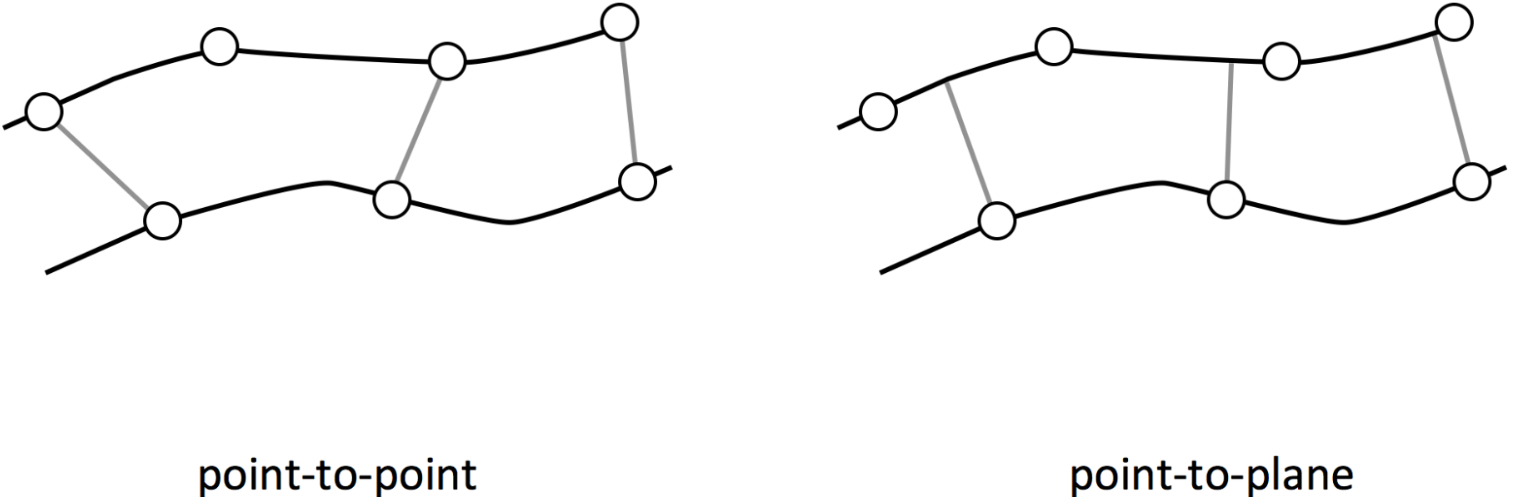
Screenshot from 2024-04-23 01-45-26

출처

위의 그림과 같이 Source point cloud인 $x_{n}$의 point와 Target point cloud $y_{n}$의 point 직접적으로 잇는 것이 아니라 target point의 가상의 평면을 만들고 normal vector를 구해 평면과 가장 가까운 점과의 거리를 최소화하는 방법

이 때, 평면을 만들기 위해서는 최소한 3개의 점이 필요하기 때문에 nearest search를 이용하여 이웃한 점들을 찾고, 이를 이용하여 normal vector 구함

아래 그림을 보면 이해하기 쉬움

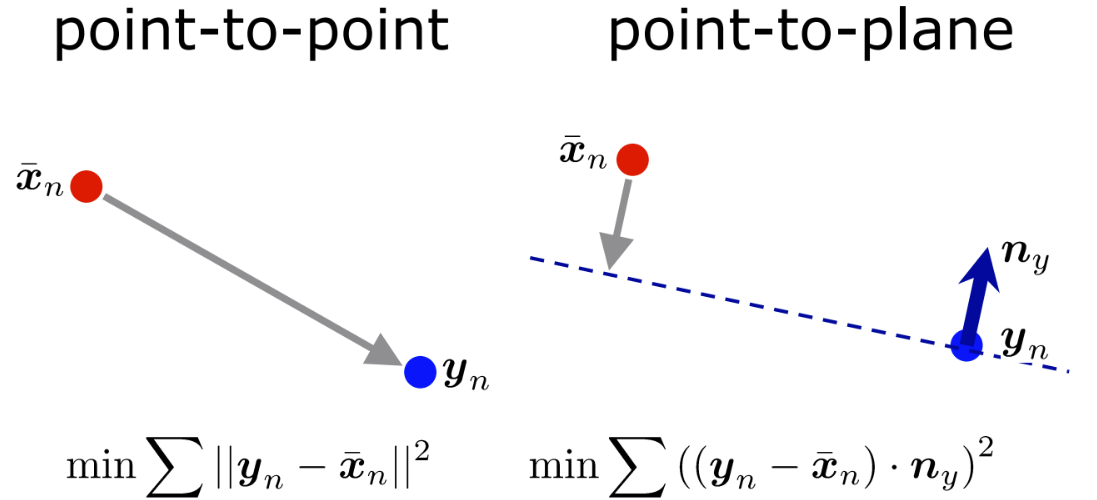
Screenshot from 2024-04-23 01-34-47

출처


Global Registration

위의 ICP 방법은 local한 registration 방법

약간 틀어진 두 개의 point cloud를 matching 가능하지만 두 point cloud의 자세가 크게 다르면 ICP를 통해 matching 할 수 없음

Global registration은 feature matching을 통해 global correspondence를 찾아 초기값에 상관없이 정합할 수 있는 알고리즘

즉, 초기값이 별도로 요구되지 않는 방법

기본적인 알고리즘은 다음과 같음


  1. Ransac을 기반으로 outlier 제거
  2. Source point cloud와 target point cloud의 feature 추출
  3. Feature를 통해 global correspondence 찾아 이를 기반으로 matching 수행


위의 알고리즘에서 보는 것과 같이 feature를 잘 추출하는 것이 핵심

좋은 feature를 이용하면 빠르게 global한 정보 registration 할 수 있음


이 방법은 local registration이 가지는 iteration 때문에 시간이 많이 소요된다는 단점을 극복함

하지만 ransac을 기반으로 outlier를 제거하는 방식 때문에 느려짐

Ransac을 사용하지 않고 일부 correspodence에 가중치를 주어 빠르게 정합을 수행하는 Fast Global Registration 방식도 존재

참고