참고

  1. https://pcl.readthedocs.io/projects/tutorials/en/latest/pfh_estimation.html
  2. https://pcl.readthedocs.io/projects/tutorials/en/latest/fpfh_estimation.html
  3. https://velog.io/@intuition/LiDAR-3D-object-detection-3-LaserNet-An-Efficient-Probabilistic-3D-Object-Detector-for-Autonomous-Driving
  4. https://robotica.unileon.es/index.php?title=PCL/OpenNI_tutorial_4:3D_object_recognition%28descriptors%29



Point Cloud 특징 추출

Harris corner 3D

Harris corner는 Computer vision에서 corner point, interest region 찾을 대 가장 기본적으로 사용하는 방법

이 방법을 3D로 확장한 방법

\[E(u, v, w)=\sum_{x,y,z\in \Omega}{[I(x+u, y+v, z+w)-I(x,y,z)]^{2}}\\\]

위 식에서 window function 생략됨

\[E(u,v,w)\approx \begin{bmatrix} u& v& w\end{bmatrix}\ M \ \begin{bmatrix}u\\ v\\ w \end{bmatrix}\] \[M=\sum_{x,y,z\in \Omega}\begin{bmatrix} I_{x}^{2} &I_{x}I_{y} &I_{x}I_{z}\\ I_{y}I_{x} &I_{y}^{2} &I_{y}I_{z}\\ I_{z}I_{x} &I_{z}I_{y} &I_{z}^{2} \end{bmatrix}\]


Harris corner 6D

x, y, z의 intensity 뿐만이 아니라 normal vector 정보를 추가하여 정확한 특징 값을 찾도록 함


ISS (Intrinsic Shape Signatures)

Covariance matrix 정의하고, 이를 기반으로 Eigenvalue Decomposition 진행하여 $\lambda_{1}$,$\lambda_{2}$,$ \lambda_{3} $ 찾음

  • $\lambda_{1}$ > $\lambda_{2}$ > $\lambda_{3}$

그리고 point에 대하여 아래의 두 조건을 만족하는 signature feature 찾음

\[\frac{\lambda_{2}(p)}{\lambda_{1}(p)} < \gamma_{12}\] \[\frac{\lambda_{3}(p)}{\lambda_{2}(p)} < \gamma_{23}\]


PFH (Point Feature Histogram)

Histogram을 기반으로 point cloud 특징을 검출하는 descriptor

아래과 같은 순서로 진행


  1. 특징을 뽑고자 하는 $p_{q}$ point에 특정 반경 $r$ 만큼의 neighborhood 선택

    img

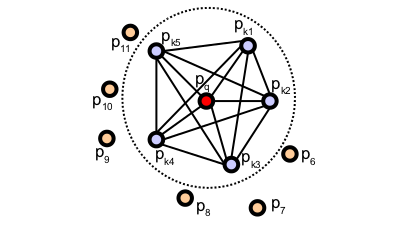
    출처

  2. $p_{q}$와 모든 neighborhood들의 connection을 연결하여 pair를 만듦

  3. 각 pair point들의 normal vector와 구해진 normal vector를 이용하여 위의 그림처럼 고정된 uvw 좌표 프레임 정의

    img

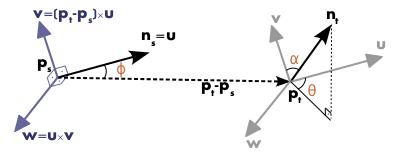
    출처

    • PCA 알고리즘을 사용하여 normal vector $n_{i}$, $n_{j}$를 구함

    • 구해진 normal vector를 이용하여 위의 그림처럼 고정된 좌표 프레임을 정의 (uvw 프레임)

      \[\begin{align} u&=n_{s}\\ v&=u\times \frac{(p_{t}-p{s})}{||p_{t}-p_{s}||_{2}} \\ w &= u\times v \end{align}\]

  4. 3에서 구한 값을 바탕으로 $f_{1}$, $f_{2}$, $f_{3}$, $f_{4}$ 계산

    \[\begin{align} f_{1}&=v \cdot n_{t}\\ f_{2}&=||p_{t}-p_{s}|| \\ f_{3}&=u\cdot (p_{t}-p_{s})/f_{2}\\ f_{4}&=atan(w\cdot n_{t}, u\cdot n_{t}) \end{align}\]

  5. $f_{1} $ ~ $f_{4}$ 을 이용하여 indexing

    \[idx=\sum_{i=1}^{i\leq 4}step(s_{i},f_{i})\cdot2^{i-1}\]
    • $s_{i}$ 값보다 $f_{i}$ 값이 크거나 같으면 1, 아니면 0
    • 0부터 15까지의 값을 가짐

  6. Index 값을 이용하여 16개의 bin을 가짐 histogram 을 기반으로 descriptor 생성


FPFH (Fast Point Feature Histogram)

img

출처


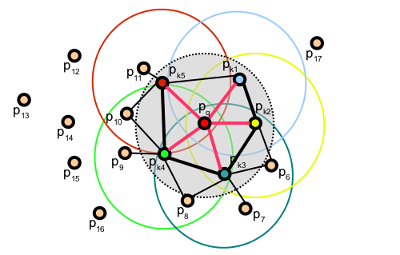
PFH는 특정 범위 안의 모든 point들의 pair에 대하여 계산한다는 단점 존재

이 문제를 해결하기 위해서 나온 방법

https://zzziito.tistory.com/m/47 참고하여 정리…


NARF (Normal Align Radial Feature)

Normal 값을 적극적으로 활용하고 있는 방법론

  1. Point Cloud를 range 이미지로 변환

    • Range 이미지는 다음에 정리 예정

  2. Range 이미지를 이용하여 물체의 경계 찾음

    Range_image_borders

    출처

  3. 찾은 경계 point로부터 normal vector 계산

  4. 경계가 아닌 곳에서 주 곡률 계산

  5. 곡률 기반으로 하여 모든 점들에 대한 특이점 (Interest point) 계산

  6. Keypoint 분리

    Range_image_NARF_keypoints

    출처

  7. 각 point에 대한 descriptor 계산


표면이 안정적이고, 근처에 주요 변화가 명백하게 있는 영역에서 NARF 사용하면 keypoint를 조금 더 정확하게 계산할수 있고 도드라지게 찾아낼 수 있음

비연속적인 변환으로 발생하는 edge 집중적으로 보면서 고려할 수 있는 방법론

참고