참고

  1. 논문



CVPR 2018

Introduction

Lidar 데이터는 신뢰할만한 depth 정보를 제공하여 객체 위치를 정확하게 파악하고, 모습을 잘 인식하는 것이 가능함

하지만 이미지 데이터와 달리 매우 sparse한 데이터를 가지고 3D 공간의 non-uniform 샘플링, 센서의 유효 범위, occlusion, 상대적인 포즈 등에 요인등에 의해 데이터의 분포가 매우 다양함

위의 문제를 해결하기 위해 다양한 방법 존재

  1. 3D object detection을 위해 조정된 point cloud의 manually crafted feature 사용하는 방법
  2. point cloud를 perspective view로 투영시켜 이미지 특징을 추출할 때 사용하는 feature extraction 적용하는 방법
  3. Point Cloud를 3D voxel grid로 rasterize하여 handcraft feature로 인코딩하는 방법

이렇게 수동으로 설계된 선택은 3D shape 정보를 효과적으로 사용하지 못하게 함

  • 2D 이미지의 recognition, detection 분야에서 hand-craft feature를 machine-learned feature로 바뀐 것이 매우 중요한 변화


PointNet과 PointNet을 발전시킨 방법이 나와 3D object detection, 3D object recognition 등에 좋은 결과 보였지만 많은 수의 point 데이터를 이용하여 네트워크를 학습해야하므로 많은 계산과 메모리가 필요

Region Proposal Network (RPN)은 효과적인 object detection을 위한 최적화 된 방법이지만 dense하고 이미지와 같이 조직화 된 구조의 데이터 필요

이 논문에서는 VoxelNet을 제안


Contribution

  • Point cloud 기반의 3D object detection을 위해 학습가능한 end-to-end deep architecture 구조인 VoxelNet 제안
  • Voxel grid에서 sparse한 point 구조와 효율적인 병렬 처리에서 모두 효과적인 VoxelNet 구현하는 방법을 제안
  • KITTI 벤치마크 데이터에 대한 실험을 하여 VoxelNet이 Lidar 기반의 자동차, 보행자, 자전거 운전자 object detection에서 SOTA의 성능을 보임



VoxelNet

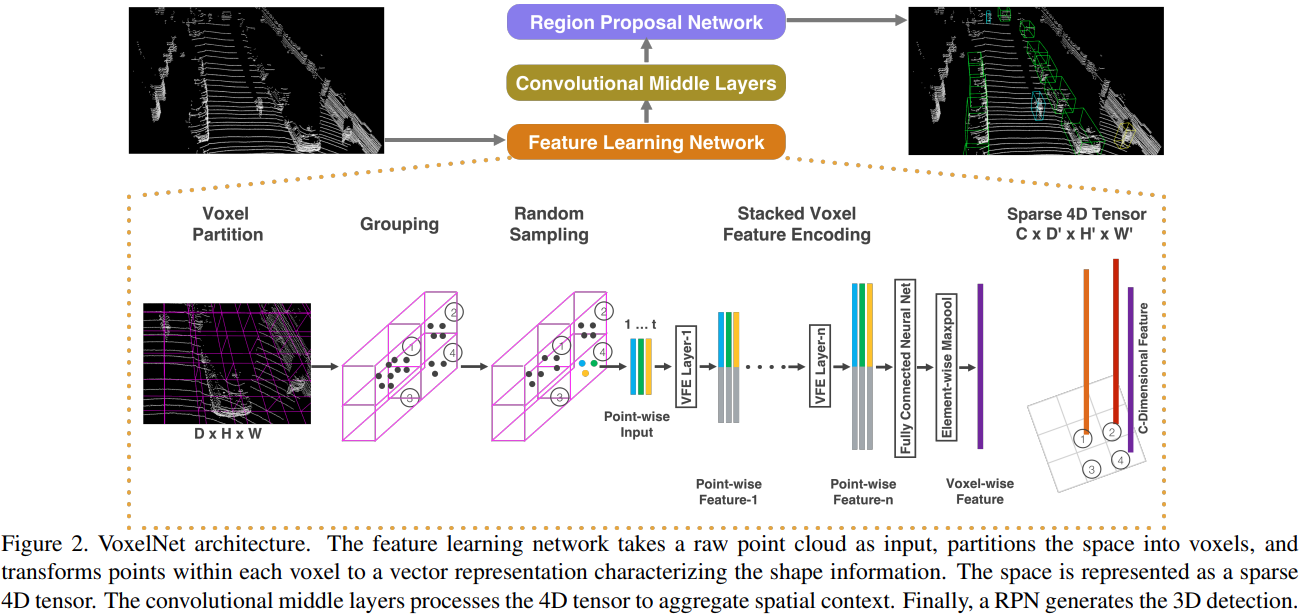
Screenshot from 2024-05-06 20-59-34


VoxelNet Architecture

VoxelNet 3개의 기능적인 블록으로 구성

  • Feature learning network
  • Convolutional middle layer
  • Region proposal network


Feature Learning Network

Voxel Partition

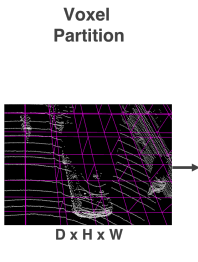
Screenshot from 2024-05-06 21-21-57

3D 공간을 동일한 크기의 voxel 사이즈로 나눔

Point cloud가 $Z$, $Y$, $X$ 축을 따라 각각 범위 $D$, $H$, $W$의 범위를 가진다고 가정

각 voxel 크기를 $v_{D}$, $v_{H}$, $v_{W}$ 라고 정의하면

결과적으로 3D voxel grid는 $D^{'}=D/v_{D}$, $H^{'}=H/v_{H}$, $W^{'}=W/v_{W}$ 로 나누어짐


Grouping

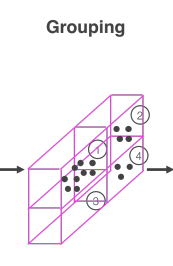
Screenshot from 2024-05-06 21-34-30

Voxel 내 존재하는 point들을 그룹화하는 과정

Point Cloud는 sparse하고 밀도 (데이터의 분포)가 매우 다양함

Voxel에서 grouping 되는 point 들의 수는 다르고 point들이 없는 경우도 존재


Random Sampling

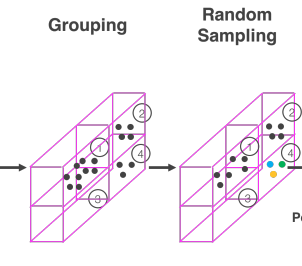
Screenshot from 2024-05-06 21-48-33

각 voxel에서 고정된 $T$ 개만큼의 random sampling

이를 통해 2가지의 목적을 이룸

  1. 계산 효율성 높임
  2. Voxel 간 point 수들의 불균형을 줄여 sampling bias를 줄이고 학습의 다양성을 부여


Stacked voxel feature encoding

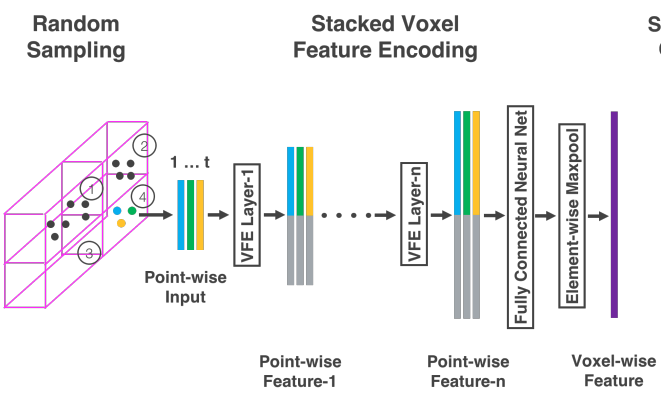
Screenshot from 2024-05-06 22-00-23

VFE (Voxel Feature Encoding) layer를 여러 개 엮어 구조를 형성

위의 그림은 하나의 voxel에 대한 계층적인 feature encoding 보여줌


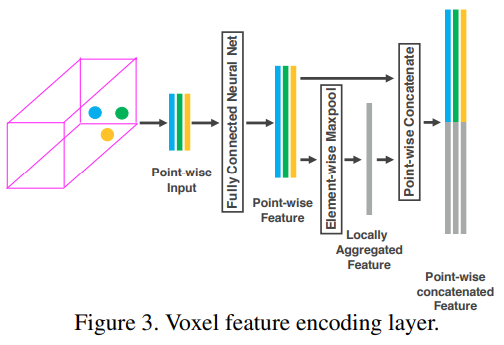
Screenshot from 2024-05-06 21-51-57


비어있지 않은 Voxel에 대해서 각 $i$ 번째 point는 아래와 같이 $XYZ$ 좌표와 received reflectance $r_{i}$ 로 구성

\[\mathbf{V}=\{ \mathbf{p}_{i}=[x_{i},y_{i},z_{i},r_{i}]^{T}\in\mathbb{R}^{4}\}_{i=1...t}\]


$\mathbf{V}$ 내에 존재하는 모든 점들의 중심으로 local mean 값을 계산하고 $v_{x}$, $v_{y}$, $v_{z}$ 로 표현

기존 $\mathbf{p}$에 중심점에 대해 상대적인 offset 을 구해 input feature set $\mathbf{V}_{in}$을 구함

\[\mathbf{V}_{in}=\{ \mathbf{\hat{p}}_{i}=[x_{i},y_{i},z_{i},r_{i}, x_{i}-v_{x}, y_{i}-v_{y},z_{i}-v_{z}]^{T}\in\mathbb{R}^{7}\}_{i=1...t}\]


각 $\mathbf{\hat{p}}_{i}$ 는 fully-connected layer를 지나 feature space $\mathbf{f}_{i}\in \mathbb{R}^{m}$로 변환

FCN layer는 linear layer, Batch Normalization layer, ReLU layer로 구성

Point-wise feature representation 을 얻은 후에 element-wise MaxPooling 을 거쳐 locally aggregated feature $\mathbf{\tilde{f}}\in\mathbb{R}^{m}$ 을 얻음

각 $\mathbf{f}_{i}$에 $\mathbf{\tilde{f}}$ 을 concat 하여 feature를 획득

모든 non-empty voxel에 대해서 같은 과정으로 encoding 되고 FCN에서 같은 parameter를 공유함


VFE-layer를 모두 통과한 후 얻은 point-wise feature를 마지막으로

Point-wise feature와 locally aggregated feature 를 결합하여 사용하기 때문에 VFE layer들은 voxel 내 point들의 상호관계에 대해 encoding 할 수 있고 final feature representation이 shape 정보를 학습할 수 있음


Sparse Tensor Representation

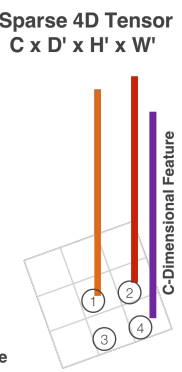
Screenshot from 2024-05-06 23-04-57


Non-empty voxel만을 처리하여 voxel의 공간 좌표와 고유하게 연관된 voxel feature 리스트를 획득

얻어진 voxel-wise feature들은 4D sparse tensor ($C\times D^{'} \times H^{'} \times W^{'}$)로 표현 가능

90%가 넘는 voxel들은 비어있기 때문에, 메모리 사용량과 계산량을 back propagation 과정 중에 줄일 수 있고, 이는 효율적인 구현에 아주 중요한 과정


Convolutional Middle Layers

아래와 같은 $M$ 차원의 convolution 적용

$\mathbf{k}$ 는 kernel 크기, $\mathbf{s}$는 stride 크기 $\mathbf{p}$ 는 padding 크기

\[ConvMD(c_{in},c_{out},\mathbf{k},\mathbf{s},\mathbf{p})\]

각 convolution middle layer는 3D convolution, Batch Normalization layer, ReLU layer 로 구성

Convolution middle layer는 receptive field를 확장해가며 voxel-wise feature를 합치고 shape description에 context를 더함


Region Proposal Network

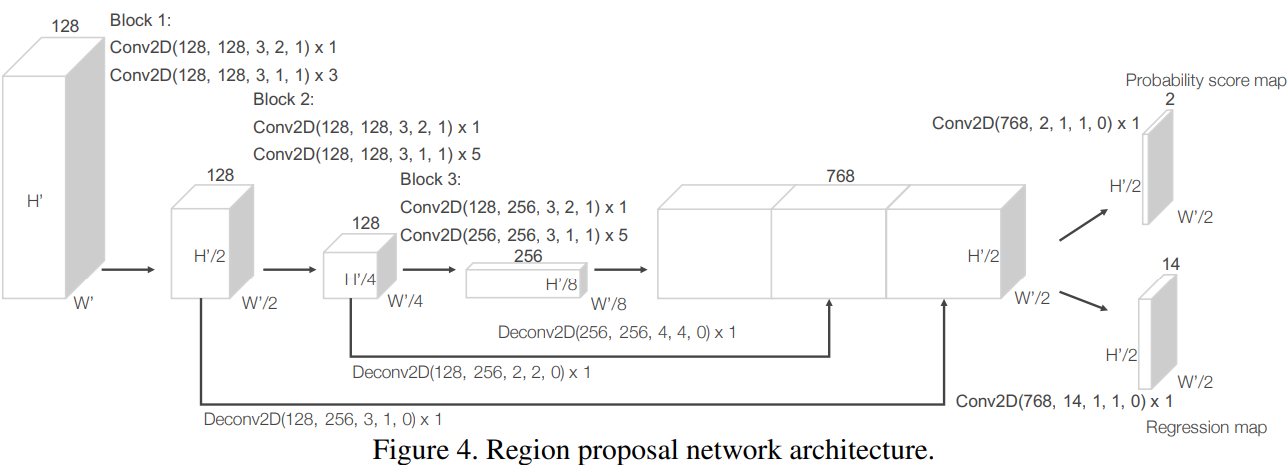
Screenshot from 2024-05-06 23-30-08

Faster RCNN에서 제시하는 RPN 구조를 수정하고 feature learning network와 convolutional middle layer와 결합하여 end-to-end 학습 파이프라인 구성


Convolution middle layer에서 나오는 feature map을 RPN의 입력으로 사용

네트워크는 3개의 convolutional layer의 block이 있고 block을 지날 때마다 feature map이 downsampling

Convolution layer를 지나고 BN, ReLU 연산이 적용됨

각 block의 output을 고정된 크기로 upsampling 하여 합친 후에 high resolution feature map을 만듦

최종적으로는 probability score map과 regression map이 나오는데 probability score map는 각 anchor 마다 하나의 scalar 값을 가지고 regression map은 각 anchor마다 7개의 scalar 가짐 ($x$, $y$, $z$, $x$, $h$, $l$, $\theta$)


Loss Function

Positive anchor set을 negative anchor set 아래와 같이 표현

\[\{ {a}_{i}^{pos} \}_{i=1...N_{pos}} \\ \{ {a}_{j}^{neg} \}_{j=1...N_{neg}}\]


  • Positive anchor는 GT box와 IoU가 특정 threshold 보다 큰 anchor 또는 가장 큰 IoU를 가지는 anchor

  • Negative anchor는 GT box와 IoU가 특정 threshold 보다 작은 anchor
  • 그 외의 경우는 무시


3D ground box는 아래와 같이 표현

\[(x_{c}^{g}, y_{c}^{g}, z_{c}^{g}, l^{g},h^{g},\theta^{g})\]
  • $x_{c}^{g}$, $y_{c}^{g}$, $z_{c}^{g}$는 중점의 좌표

  • $l^{g}$, $h^{g}$, $\theta^{g}$는 box의 길이, 너비, 높이

  • $\theta^{g}$는 $Z$ 축의 yaw 회전을 나타냄


매칭된 positive anchor에 대하여 아래와 같이 정의

\[(x_{c}^{a}, y_{c}^{a}, z_{c}^{a}, l^{a},h^{a},\theta^{a})\]


Positive anchor에 대하여 regression loss를 계산하고 regression map이 residual 값들 출력하도록 학습

Residual vector $\mathbf{u}^{*}$는 아래와 같은 값들로 구성

\[\Delta x=\frac{x_{c}^{g}-x_{c}^{a}}{d_{a}},\ \ \Delta y=\frac{y_{c}^{g}-y_{c}^{a}}{d_{a}}, \ \ \Delta z=\frac{z_ {c}^{g}-z_{c}^{a}}{d_{a}}\\ \Delta l=log(\frac{l^{g}}{l^{a}}), \ \ \Delta w=log(\frac{w^{g}}{w^{a}}), \ \ \Delta h=log(\frac{h^{g}}{h^{a}}) \\ \Delta \theta = \theta^{g}-\theta^{a}\]
  • $\Delta x$, $\Delta y$, $\Delta z$는 중심 좌표
  • $\Delta l$, $\Delta w$, $\Delta h$는 box의 길이, 너비, 높이
  • $\Delta \theta$는 회전
  • $d^{a}=\sqrt{(l^{a})^{2}+(w^{a})^{2}}$


위에서 구한 값들로 아래와 같은 Loss function 구성

\[\begin{align} L&=\alpha \frac{1}{N_{pos}}\sum_{i} L_{cls}(p_{i}^{pos}, 1) + \beta \frac{1}{N_{neg}}\sum_{j} L_{cls}(p_{j}^{neg}, 0) \\ &+\frac{1}{N_{pos}}\sum_{i}L_{reg}(\mathbf{u}_{i}, \mathbf{u}_{i}^{*}) \end{align}\]
  • $p_{i}^{pos}$, $p_{j}^{neg}$ 는 positive anchor $a_{i}^{pos}$, $a_{j}^{neg}$의 softmax 결과
  • 앞의 두 term은 정규화된 binary cross entropy loss
  • $L_{reg}$는 SmoothL1 loss


Efficient Implementation

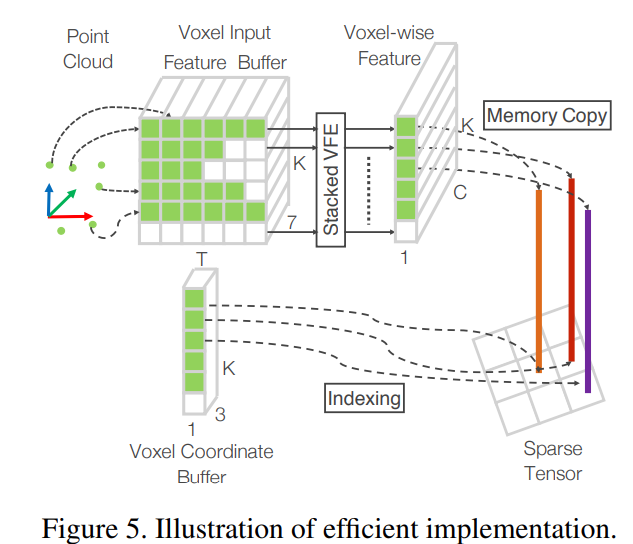
Screenshot from 2024-05-07 01-03-43



Training Detail

Network Details

논문 참고


Data Augmentation

학습 point cloud의 수가 4000개 미만이면, overfitting이 발생하는데 이를 줄이기 위해 3가지 다른 data augmentation 적용


각 3D GT box에 perturbation을 독립적으로 적용하는 방법

Bounding box의 중점을 기준으로 rotation하고 $(x, y, z)$ 방향으로 각각 평균이 0이고 분산ㄴ이 1인 가우시안 분포에서 샘플링한 만큼 translation 적용


[0.95, 1.05]의 uniform 분포에서 값을 샘플링하여 모든 GT box의 전체 point cloud에 global scaling 적용

다양한 거리에 있고 크기를 가지는 object에 대하여 detection을 할 수 있도록 도움


모든 GT boxd의, 전체 point cloud에 대하여 $Z$ 축으로 원점 (0, 0, 0) 을 중심으로 rotation 적용



Experiments

VoxelNet을 KITTI 3D object detection 벤치마크 데이터로 평가


Evaluation on KITTI Validation Set

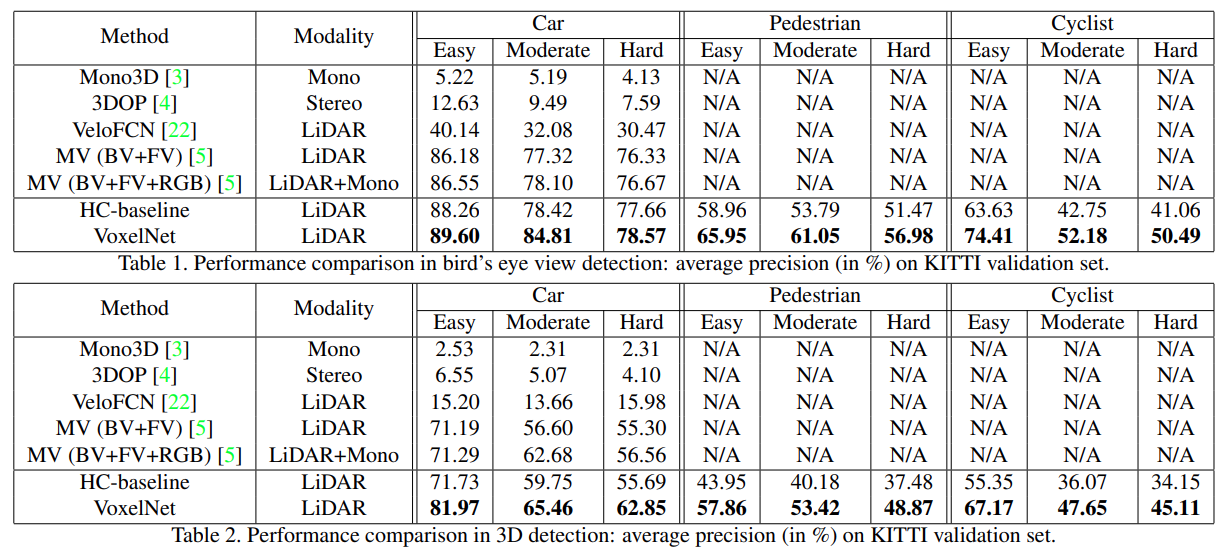
Screenshot from 2024-05-07 01-23-52

  • 3D detection, bird’s eye view 둘 모두 단일 LiDAR 데이터만을 이용해도 성능이 가장 좋음을 확인


Evaluation on KITTI Test Set

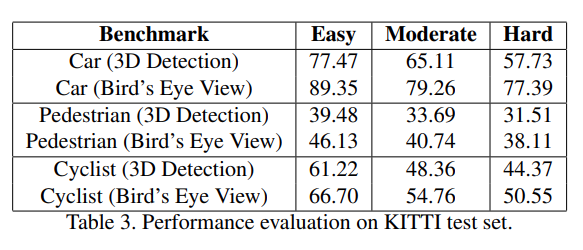
Screenshot from 2024-05-07 01-28-52

  • Bird’s eye view를 이용하면 성능이 더 좋아짐을 확인



Conclusion

Voxel grouping을 통해 point cloud의 3차원 object detection 방법 제안

그룹화된 voxel을 encoding 할 수 있는 네트워크 제시

Convolution layer, RPN 사용

KITTI dataset에서 기존 방법 대비 성능이 향상됨을 확인

참고