참고

  1. 논문



Patchwork++: Fast and Robust Ground Segmentation Solving Partial Under-Segmentation Using 3D Point Cloud

2022

Introduction

다양한 학습 기반의 3D perception 방법들이 좋은 성능을 보였으나 2가지 문제점이 존재

  1. 학습 기반의 방법은 사람이 point-wise labeling 을 수행해야하기 때문에 시간이 오래 소요
  2. 학습 기반의 segmentation은 학습 데이터셋에서 얻는 scene이 다르거나 센서 구성이 다른경우 성능이 떨어짐

따라서 ground segmentation에서 non-learning 기반의 방법에 초점을 맞춤


일반적으로 ground segmentation은 전처리 단계로 많이 사용되는데 이를 위해 3가지 조건을 만족해야 함

  1. 다른 알고리즘을 적용하기 전에 전처리로 사용하기 위해서는 속도가 빨라야 함
  2. Precision과 recall을 보장하기 위해 성능의 변동이 거의 없어야 함
  3. Ground가 고르지 않은 야외 환경도 대처할 수 있어야 함


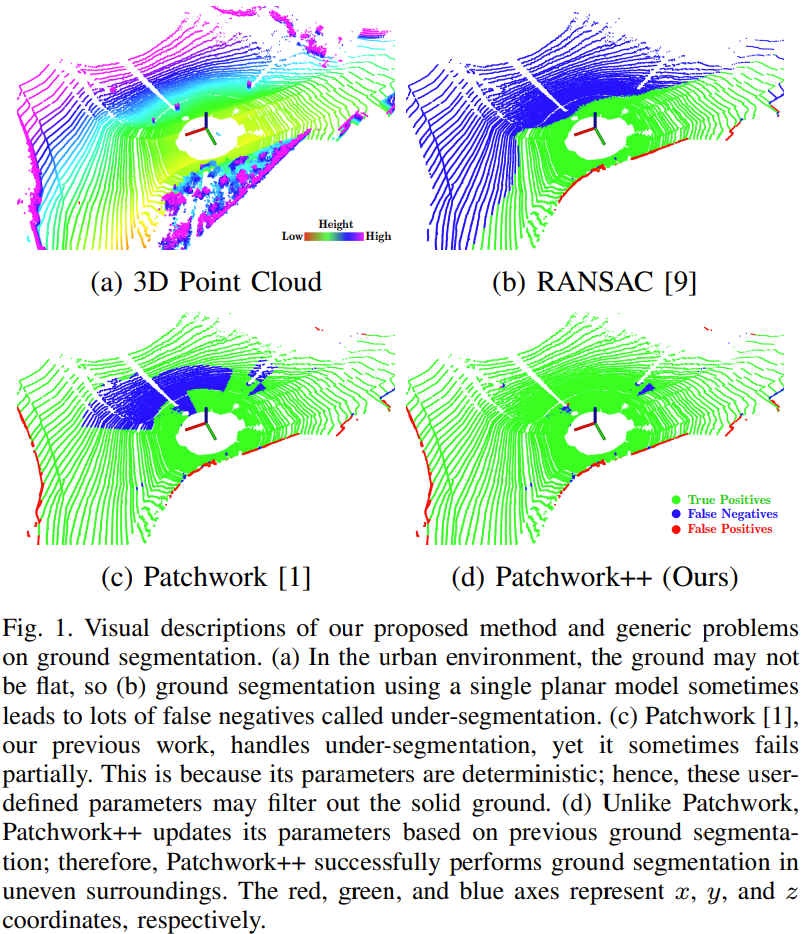
Screenshot from 2024-05-16 09-18-59


Fig 1(b) 에서 보는 것과 같이 몇몇 방법들은 이 조건들을 만족시키지 못하고 segmentation을 잘 하지 못하는 문제가 발생

Fig 1(c) 는 조건들을 다 만족시키나 부분적으로 segmentation을 잘 하지못하는 문제 발생

이러한 under-segmentation 문제에는 2가지 원인이 있음

  1. 일부 방법들은 deterministic 함
  2. 낮은 $z$가 ground point가 될 가능성이 높다는 가정이 성립하지 않는 경우 존재


이를 위해 Patchwork를 개선한 Patchwork++ 제안하여 다음과 같은 기여를 함

  • Adaptive ground likelihood estimation (A-GLE) 와 temporal ground revert (TGR)으로 coarse-to-fine 전략을 취하여 부분적으로 under-segmentation이 되는 문제를 해결하여 FN을 줄임
  • 2가지의 새로운 outlier rejection module을 제시하여 noise나 non-ground point를 거부하도록 함
    • Reflected Noise Removal (RNR)
    • Region-wise Vertical Plane Fitting (R-VPF)
  • SemanticKITTI 데이터셋을 사용하여 기존의 SOTA 방법과 비교하여 빠른 속도로 좋은 성능을 내는 것을 확인



PATCHWORK++: FAST, ROBUST, AND ADAPTIVE GROUND SEGMENTATION

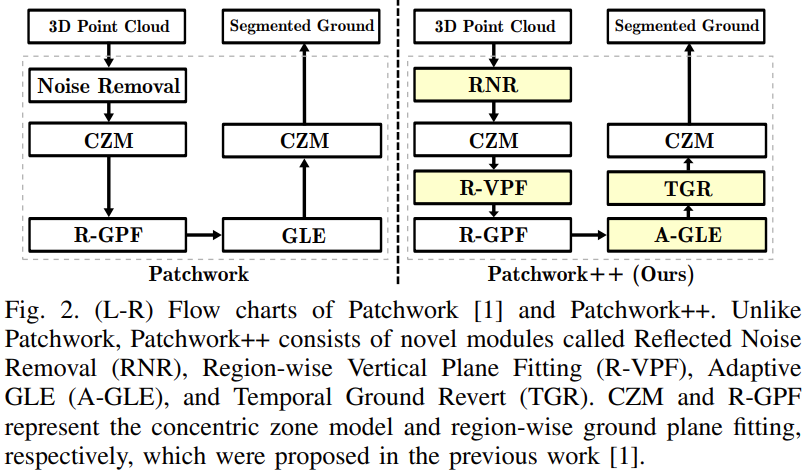
Screenshot from 2024-05-16 09-38-03


RNR: Reflected Noise Removal

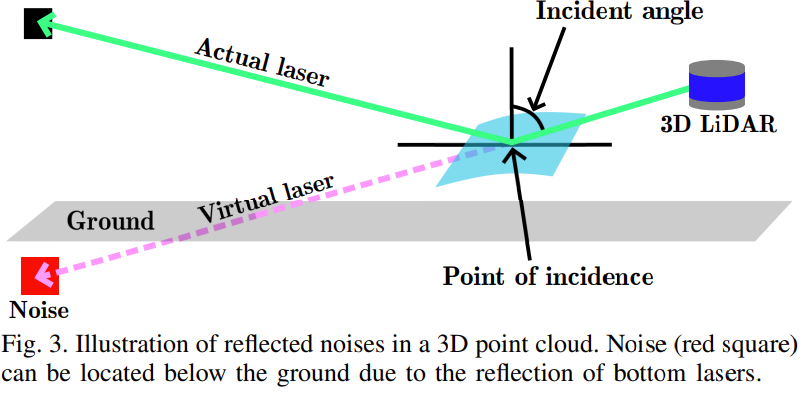
Screenshot from 2024-05-16 09-41-41


Fig. 에서 보는 것과 같이, noise는 종종 실제 ground 밑에서 발생

하지만 R-GPF는 bin에서 가장 높이가 낮은 point을 ground point라고 가정하고 초기의 seed를 선택하여 noise들도 초기 seed에 포함되었고 이로 인해 under-segmentation 문제 발생


이 문제를 해결하기 위해 $z$ 값이 사용자가 지정한 threshold인 $z_{min}$ 보다 작은 경우 이 point를 제거하면서 필터링

하지만 이런 noise 제거 방법은 급경사 환경에서 실제 ground point를 제거한다는 문제 발생


Screenshot from 2024-05-16 09-51-40


Fig 4. (b), (c)에서 이를 확인 할 수 있음

그래서 실제 ground point와 noise를 구별할 수 있어야 함


구별 할 수 있도록 RNR은 2가지 중요한 관찰에 대한 내용을 바탕으로 제안됨

첫 번째는 가상의 noise가 반사 표면으로 부터 얻어진다는 점

  • 자동차의 보넷이나 천장 또는 유리 등

Noise point들은 센서 원점에서 입사 지점까지의 방향에 따라 위치함 (Fig. 3)

입사각이 작을수록 noise들의 $z$값이 더 작아짐

즉, 입사각이 크면, noise가 ground point와 비슷한 유사한 위치에 존재한다는 의미

LiDAR에서 발생하는 치명적인 noise들은 LiDAR의 하단의 ring에서 발생

  • **여기에서 하단 ring의 입사각이 작다고 하는데,, 큰게 아닌가..?ㅠㅠ **


두 번째는 noise point의 ray는 센서로 돌아올 때까지 더 많은 반사를 겪기 때문에 일반적인 point보다 intensity가 낮음


RNR은 noise point를 제거하기 위해 특정 개수 $N_{noise}$의 하단 링 확인

이 링들에서 noise removal height threshold $h_{noise}$ 보다 낮은 곳에 위치하고 noise removal intensity threshold $I_{noise}$ 보다 낮은 intensity를 가지는 point를 noise로 간주하고 제거

$h_{noise}$ 는 A-GLE를 통해 업데이트 됨


R-VPF: Region-wise Vertical Plane Fitting

수직의 도시 구조물이 았는 경우 R-GP는 적절한 ground plane을 추정하는 것이 힘듦

수직의 구조물들은 실제 ground point와 비교하여 더 작은 $z$ 값을 가지고 있기 때문에 초기의 seed 값으로 선택되기 때문


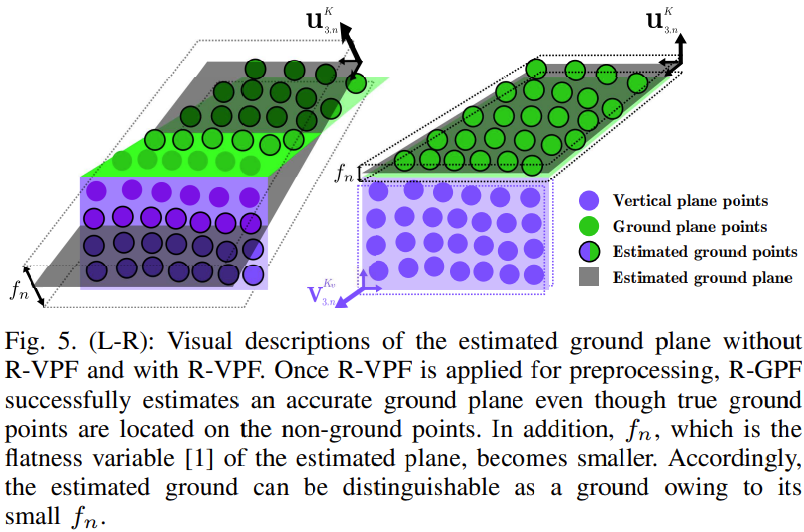
Screenshot from 2024-05-16 10-53-25


PCA 방식은 outlier 취약하기 때문에 잘못된 ground plane을 찾음


이를 위해 R-VPF를 제안하여 R-GPF가 bin 내의 주요 수직 point를 제거하여 보다 정확한 ground plane을 추정 가능하도록 함

CZM 으로 나누어진 $n$ 번째 bin의 point들을 $P_{n}$ 이라 표기

추정된 수직 평면 point를 $\hat{V}_{n}$

4가지 단계를 거쳐 수직면을 추정

첫번째로 R-VPF은 매 $k$번째 iteration마다 최저점 point들을 seed point들로 선택

그 후 seed point들의 평균 \(\mathbf{m}^{k}_{n}\in \mathbb{R}^{3}\) 과 PCA로 얻은 \(\mathbf{v}^{k}_{3, m}\) 을 계산한

$k$ 번째 잠재서 수직면을 다음과 같은 방법으로 샘플링

\[\hat{W}^{k}_{n} =\{\mathbf{p}\in \hat{P}^{k}_{n} \ | \ |(\mathbf{p}-\mathbf{m}^{k}_{n})\cdot \mathbf{v}^{k}_{3, m}|<d_{v} \}\]
  • $d_{v}$ : 추정된 수직면의 distance margin

위의 식에서 $k=1$ 일 때는 \(\hat{P}^{k}_{n} \leftarrow P_{n}\) 이고 그 외에는 \(\hat{P}^{k}_{n} \leftarrow P_{n}-\bigcup_{i=1}^{k-1}\hat{V}_{n}^{i}\)

이 전 iteration에서 수직 점으로 추정된 점들이 다음 iteration에서 제거됨을 의미


$\hat{V}_{n}^{k}$ 은 $k$ 번째 iteration에서의 수직 point들이고 다음과 같이 구함

\[\hat{V}_{n}^{k}=\left\{\begin{aligned} &\hat{W}^{k}_{n}, \ if \ \frac{\pi}{2}-cos^{-1}(\mathbf{v}_{3, n}^{k} \cdot \mathbf{u}_{z}) < \theta_{v} \\ & \O , \ otherwise \end{aligned}\right.\]
  • $\mathbf{u}_{z}$ : z축 방향의 unit normal vector, $[0\ 0\ 1]^{T}$
  • $\theta_{v}$ : 추정된 평면의 unit normal vector에 대한 margin


마지막으로 추천된 모든 수직 point들 $\hat{V}_{n}$은 다음의 식과 같이 구함

\[\hat{V}_{n}=\bigcup_{k=1}^{K_{v}}\hat{V}_{n}^{k}\]
  • $K_{v}$ : R-VPF의 iteration 수


A-GLE: Adaptive Ground Likelihood Estimation

기존의 Patchwork에서는 GLE을 사용하여 uprightness, elevation, flatness 이 세 가지 요소로 ground인지 non-ground 인지 결정

$\theta_{\tau}$, $k(r_{n})$, $\sigma_{\tau, m}$ 은각각patchwork의 uprightness, elevation, flatness 의 threshold

이 실험에서는 간단하게 seed point들의 평균인 \(\bar{z}_{n}\), $\sigma_{n}$, $k(r_{n})$, $\sigma_{\tau, m}$을 $e_{n}$, $f_{n}$, $e_{\tau, m}$, $f_{\tau, m}$ 으로 나타냄

우리의 이전 연구에서 최적의 파라미터를 정할 때, 특히 $e_{\tau, m}$, $f_{\tau, m}$ , 주변 환경에 의존하여 시간이 오래 소모되었음

  • Scene 마다 다르게 설정


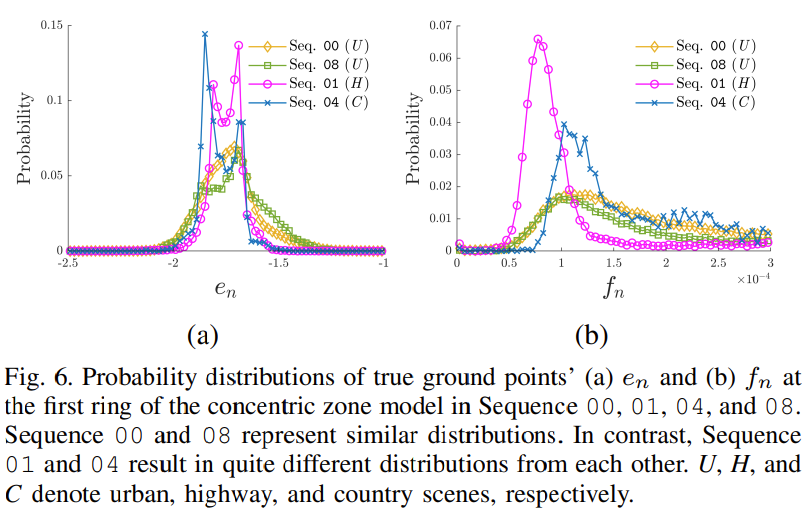
Screenshot from 2024-05-16 12-27-40


Fig. 6에서처럼 주변 환경에 따라 실제 ground plane의 elevation value와 flatness value 분포가 달라짐을 확인

따라서 각 환경마다 파라미터 조절이 필요하다는 것을 확인


Elevation

파라미터를 스스로 업데이트 시키기 위해 새로운 컨셉인 definite ground $D_{m}$을 도입

이는 CZM의 $m$ 번째 ring에서 이전에 추정된 uprightness와 elevation을 만족하는 ground plane을 의미

A-GLE는 definite ground plane의 평면을 사용하여 다음 추청을 위한 elevation 파라미터를 업데이트


$E_{m}$은 추정된 $D_{m}$ 평면에서의 모든 $e_{n}$ 값들의 집합

$E_{m}$을 바탕으로 $e_{\tau, m}$ 은 다음과 같이 업데이트 됨

\[e_{\tau, m} \leftarrow mean(E_{m})+a_{m}\cdot stdev(E_{m})\]
  • $a_{m}> 0$ : CZM 모델의 $m$ 번째 ring의 elevation에 대한 표준편차 항의 gain 상수


Flatness

이전 Patchwork의 계산에서 잠재적인 문제가 있음을 팔견

기존에는 $f_{n}$이 \(\frac{\lambda_{3, n}}{\lambda_{1, n}+\lambda_{2, n}+\lambda_{3, n}}\) 으로 계산

이 방식으로 의미있는 값을 얻기 위해서는, ground의 상대적인 LiDAR 위치와 상관없이 같은 ground에서는 일관된 결과를 얻어야 함


Patchwork는 CZM을 이용하므로, ground는 센서의 origin을 중심으로 하는 bin으로 나누어지고, ground를 나누기 위해 사용된 방법에 따라 모양과 크기가 달라짐

$\lambda_{1, n}$과 $\lambda_{2, n}$ 는 전반적인 ground가 변하지 않는데도 변할 수 있음

이로 인해 $f_{n}$은 잠재적인 불일치를 바탕으로 하기 때문에 비논리적이라고 할 수 있음

이 문제를 해결하기 위해서 Patchwork++ 는 $f_{n}=\lambda_{3, n}$, 표면의 normal vector의 변화라고 설정


$e_{\tau, m}$과 비슷하게 $f_{\tau, m}$도 $D_{m}$ 의 분포를 기반으로 A-GLE를 사용하여 업데이트

$F_{m}$은 $D_{m}$ 에서 추청된 평면에 대한 모든 $f_{n}$ 값들의 집합

\[f_{\tau, m} \leftarrow mean(F_{m})+b_{m}\cdot stdev(F_{m})\]
  • $b_{m}> 0$ : CZM 모델의 $m$ 번째 ring의 flatness에 대한 표준편차 항의 gain 상수


Noise Removal Height

A-GLE는 $h_{noise}$는 CZM 의 가장 가까운 ring에서 추정된 ground plane의 elevation 값들의 평균을 바탕으로

\[h_{noise}\leftarrow mean(E_{1})+\delta\]
  • $\delta < 0$ : noise removal의 distance margin


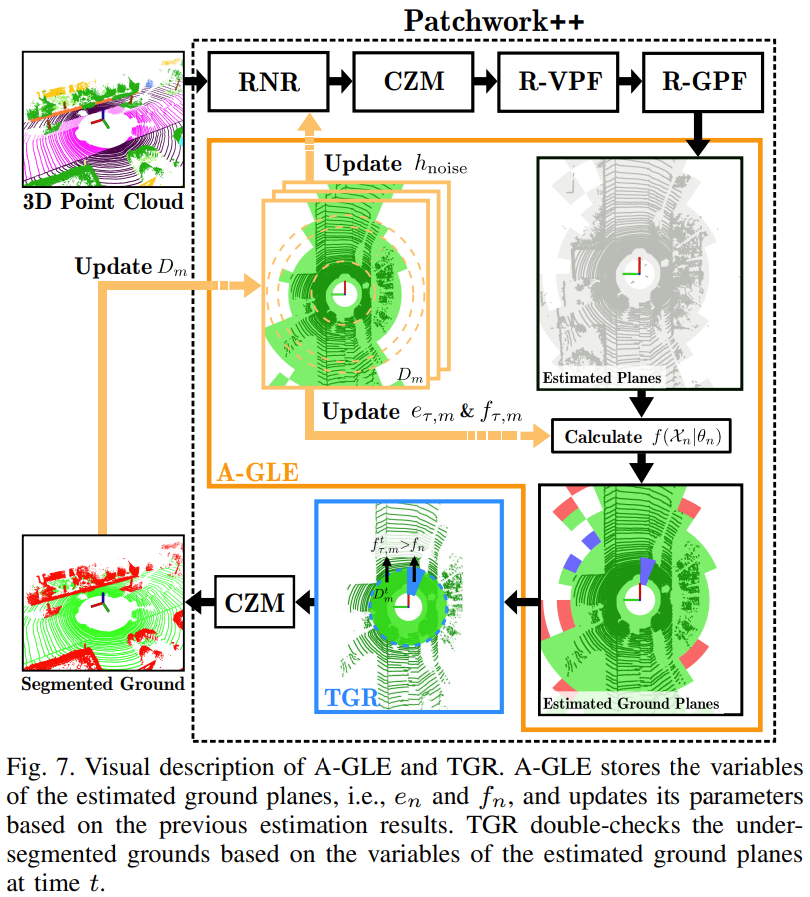
Screenshot from 2024-05-16 16-42-52


Fig. 7은 A-GLE의 과정을 나타냄


TGR: Temporal Ground Revert

Bin 안의 어떤 특이한 ground point들은 파라미터의 조건을 만족하지 않음

예를 들어 잔디가 있는 거친 지형은 종종 자체 업데이트 된 파라미터보다 높은 $e_{n}$, $f_{n}$ 값을 가짐

A-GLE는 시간이 지남에 따라 모든 값을 이용하여 파라미터를 업데이트 하기 때문인데 이는 A-GLE를 low-pass fileter의 역할을 하게 만듦

이는 $f_{n}$의 값이 일시적을 커지면 bin을 ground로 추정하기 어렵게 만듦


TGR은 $D_{m}^{t}$를 이용하여 under-segmented ground plane을 segmented ground bin으로 되돌릴 있도록 제시됨

$D_{m}^{t}$는 $t$ 시점에서의 definite ground plane

정리하자면, TGR은 각각의 under-segmented된 bin들의 $f_{n}$을 $f_{\tau, m}^{t}$ 와 비교함

$F^{t}{m}$은 $D{m}^{t}$에서의 $f_{n}$들의 집합

\[f_{\tau, m}^{t}=mean(F^{t}_{m})+c_{m}\cdot stdev(F^{t}_{m})\]
  • $c_{m}> 0$ : CZM 모델의 $m$ 번째 ring의 표준편차 항의 gain 상수

$f_{n}$이 $f_{\tau, m}$보다 커서 제거된 ground point가 $f_{n}$ < f_{\tau, m}^{t} 라는 조건을 만족하면 다시 되돌릴 수 있음



RESULTS AND DISCUSSION

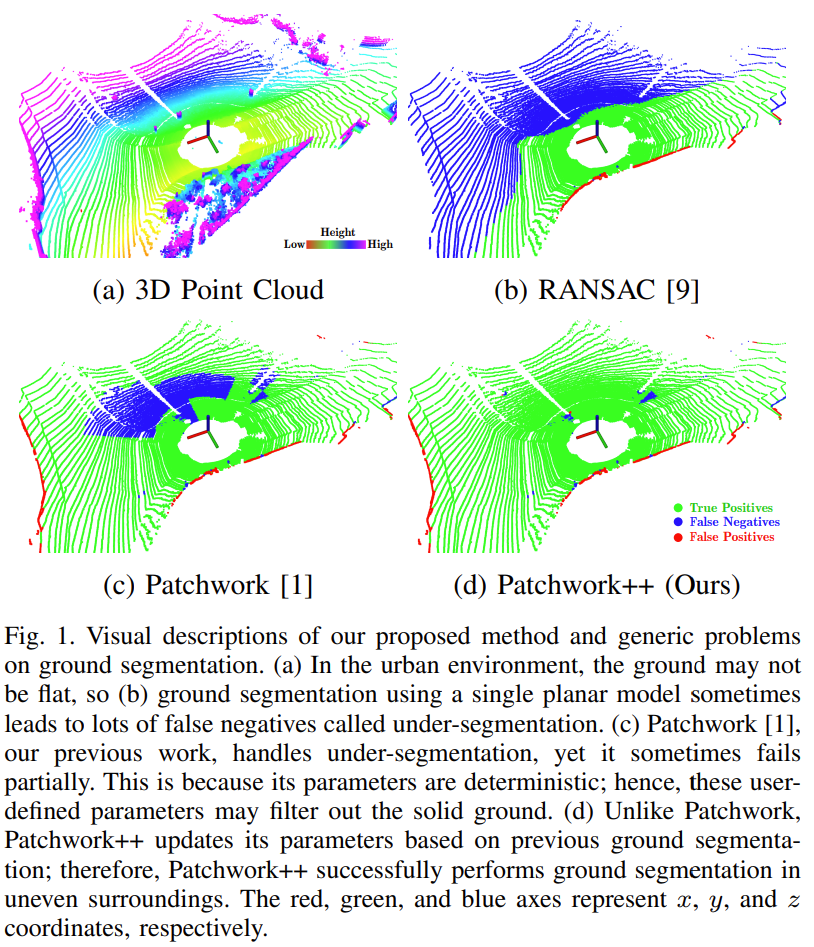
Screenshot from 2024-05-16 17-21-33

  • RANSAC 방법을 이용한 경우 결과가 좋지 않음
  • Patchwork, Patchwork++ 를 이용ㅇ하는 경우 FN의 수가 줄어드는 것을 확인
  • Patchwork++는 Patchwork보다 FN의 수를 많이 줄임


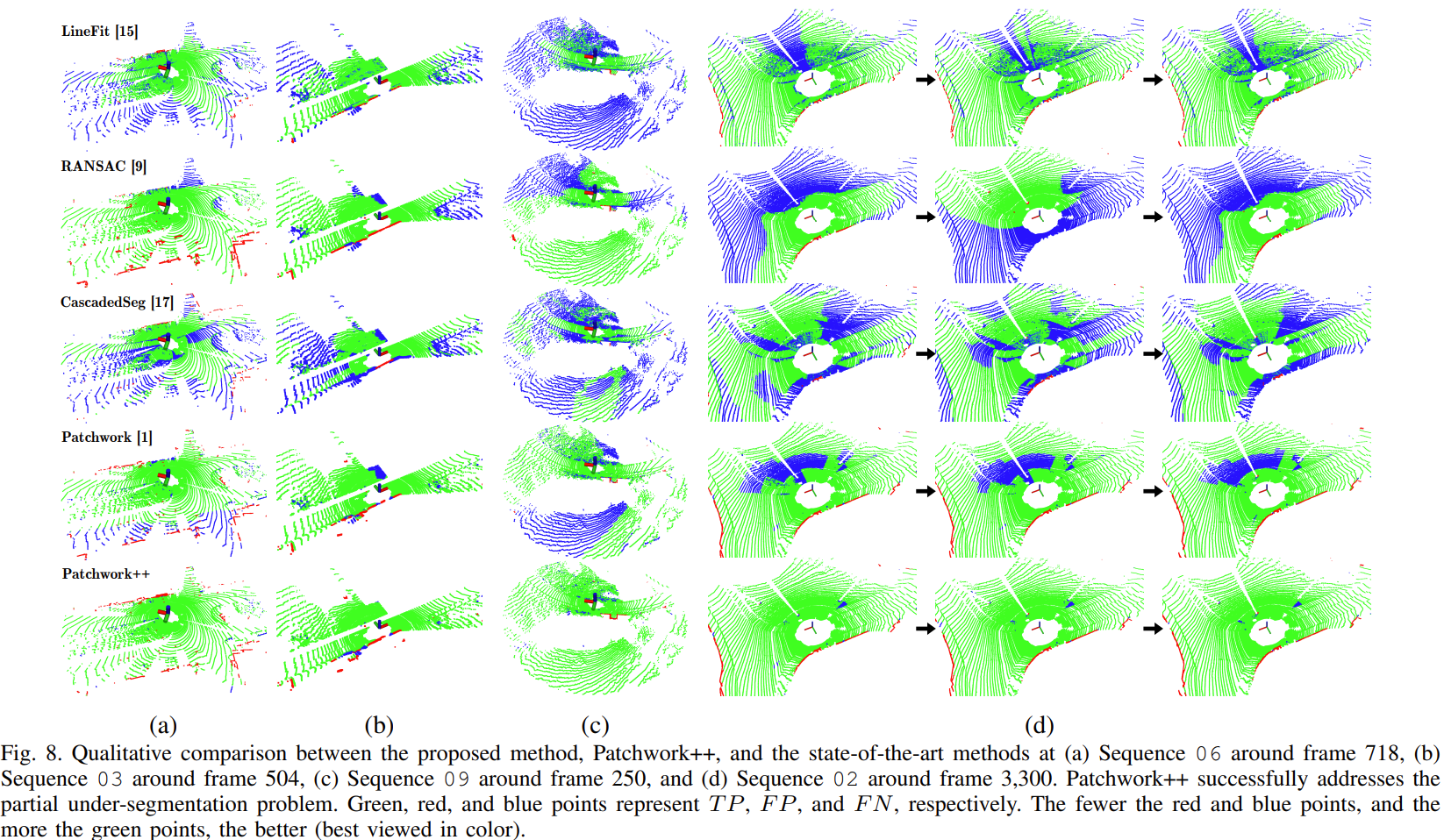
Screenshot from 2024-05-16 17-26-03

  • FN가 다른 방법들에 비해 Patchwork++가 확연하게 좋아짐을 확인


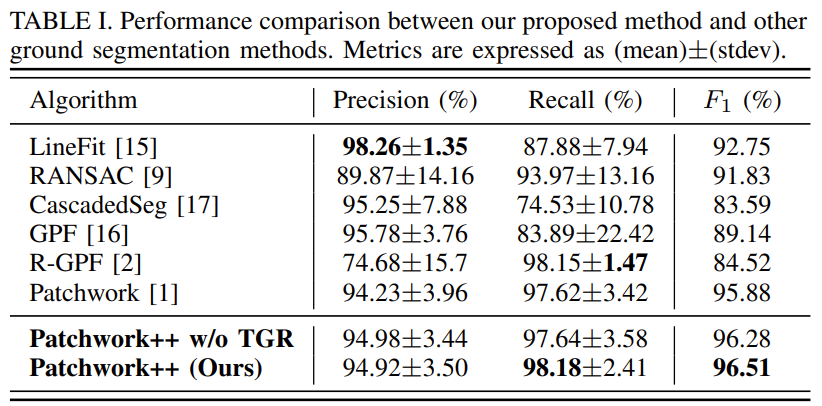
Screenshot from 2024-05-16 17-32-42

  • Precision을 LineFit이 가장 좋으나 Recall에 대해서는 성능이 좋지 않음을 확인
  • Patchwork++은 상대적으로 안정적인 Precision의 결과를 얻고, recall도 좋은 결과를 얻음
  • 최종적으로 가장 좋은 F1 score 를 가짐
  • TGR 적용 유,무에 따라 Recall 값이 좋아짐을 확인


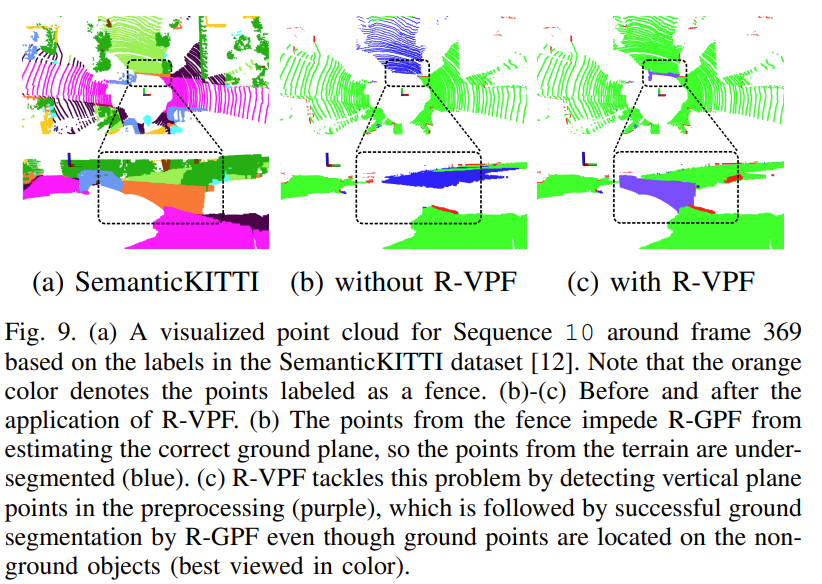
Screenshot from 2024-05-16 17-38-04

  • R-VPF을 사용하면 under-sesgmentation된 지형도 잘 segmentation 하는 것을 확인
  • 또한 R-VPF를 사용하면 수직 평면이 잘 fitting 됨을 확인


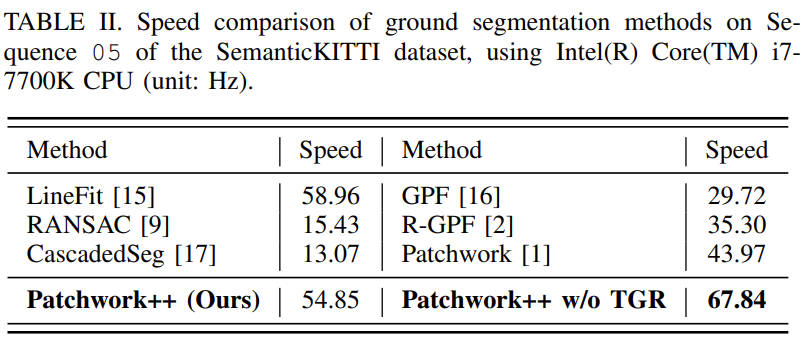
Screenshot from 2024-05-16 17-44-23

  • LineFit과 유사한 속도로 Patchwork++가 작동
  • 기존의 Patchwork보다 속도가 빨라짐
  • TGR을 빼고 Patchwork++를 적용했을 때는 13Hz 가 증가함



CONCLUSION

기존의 Patchwork를 개선하기 위한 방법 제시

Adaptive한 GLE 업데이트와 Temporal ground revert 방법 적용

Reflected noise removal과 vertical plane fitting으로 outlier 줄임

기존 SOTA 방법들과 비교하여 높은 정확도의 ground segmentation이 가능

참고