참고

  1. 논문



Patchwork: Concentric Zone-based Region-wise Ground Segmentation with Ground Likelihood Estimation Using a 3D LiDAR Sensor

Introduction

이 논문에서는 ground segmentation 에 초점을 맞춤

Segmentation의 목적은 크게 2가지

  1. 성공적인 탐색을 위한 이동 가능한(movable) 영역 추정
  2. 다른 움직이는 object를 인식하거나 추적하기 위함

지상 차량이나 사람들은 필수적으로 지면과 연결

이상적으로 지면이 잘 추정되는 경우에는 간단하게 Euclidean clustering 같은 방법으로 움직이는 물체를 인식할 수 있음

또한, 대부분의 point cloud는 지면에 있기 때문에 object detection이나 segmentation을 적용하기전에, 전처라 방법으로 ground segmentation 을 사용하면 계산량을 크게 줄일 수 있음

따라서, 이 연구에서의 지면은 이동가능한 도로뿐만이 인도나 잔디밭을 포함하여 움직이는 객체가 접촉할 수 있는 모든 영역을 의미


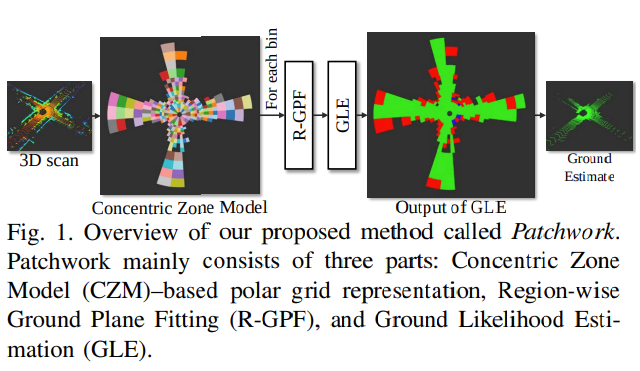
Screenshot from 2024-05-14 11-05-12


Patchwork라고 하는 새로운 Concentric Zone Model (CZM) 기반의 region-wise ground segmentation 방법 제시

  • 이 저자들의 이전 연구인 Region-wise Ground Plane Fitting (R-GPF) 의 확잔된 연구


이 논문의 contribution은 아래와 같음

  • SemanticKITTI 데이터 셋을 이용한 복잡한 도시 환경에서의 지면을 추축을할 때 bin의 사이즈의 영향을 최초로 분석했다는 주장
    • 효율적이고, nonuniform한 3D point cloud의 region-wise representation 제시 가능
    • CRM 기반의 representation이라하며 각 영역 (zone)에 따라 bin 크기가 다름
  • 각 bin이 지면과 접촉되어 있는지 결정하기 위해서 uprightness, elevation, flatness 관점에서 Ground Likelihood Estimation (GLE) 를 활용
  • 40Hz 이상에서 SOTA의 region-wise fitting 기반의 방법보다 좋은성능을 보여줌



METHODOLOGY OF PATCHWORK

Patchwork는 크게 3 부분으로 구성

  • CZM
  • R-GPF
  • GLE


Problem Definition

$N$개의 point들로 구성된 point cloud는 \(P=\{\mathbf{p}_{1}, \mathbf{p}_{2}, ..., \mathbf{p}_{k}, ..., \mathbf{p}_{N}\}\) 로 표시함

각 point $\mathbf{p}_{k}$는 \(\{x_{k}, y_{k}, z_{k}\}\) 좌표로 구성됨

이 논문에서 $P$는 2개의 class로 분류됨

  • $G$ : ground point
  • $G^{C}$ : ground point가 아닌 점, 즉 $G$의 여집합


추정된 ground point는 $\hat{G}$라고 표현하고 추정된 값을 오류를 포함할 수도 있음

\[\hat{G}=TP\ \cup \ FP \ \ and \ \ \hat{G}^{c}=FN \ \cup \ TN\]

목표는 $FP$와 $FN$가 적은 ground segmentation 수행하는 것


Concentric Zone Model

Ground가 flat하지 않기 때문에 추정 할 때 전체 영역을 한번에 보기보다는 작은 영역이나 bin으로 나누어 ground영역인지 아닌지 추정


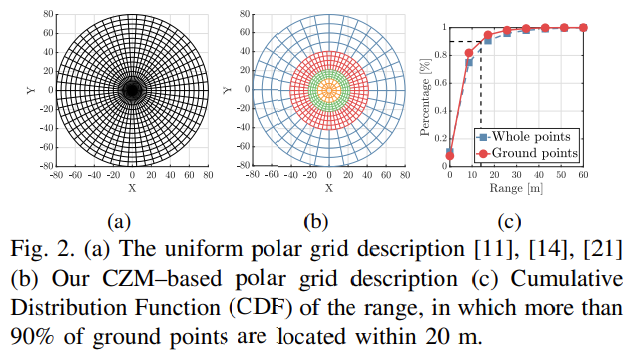
Screenshot from 2024-05-14 11-09-44

Fig. 2의 (a) 처럼 기존의 cloud point를 반지름과 방위각 방향, 즉 ring과 sector 로 일정한 간격으로 균등하게 나눈 여러개의 빈으로 나누는 polar grid representation (또는 $S$) 이용


하지만 Fig.2 (c)에서 보는 것 처럼 대부분의 ground point들은 센서 가까이에 위치한다는 것을 실험적으로 할 수 있음

즉 90%가 넘는 point들은 20m 내에 존재


위와 같은 이유로 $S$ 2가지 한계 존재

  1. Sparsity issue
    • 거리가 멀어질수록 올바른 ground plane을 찾기에는 point cloud가 매우 sparse 해짐
  2. Representability issue
    • 중심 (origin) 에 위치한 bin의 크기가 unit space를 표현하기 너무 작은 경우에는 ground plane의 올바른 normal vector 추정이 어려움


위의 문제를 해결하기 위해 CZM 기반의 polar grid representation $C$ 제시

Fig 2. (b) 에서처럼, $P$는 크기가 다른 bin으로 구성된 영역들로 나누어짐

\(<N>={1, 2, ..., N}\) 으로 표현하고 제안한 모델은 다음과 같이 정의돔

\[C=\bigcup_{m\in<N_z>}Z_{m}\]
  • $Z_{m}$ : $C$의 $m$ 번째 zone
  • $N_{Z}$ : Zone의 개수, 이 논문에서는 4개


\[Z_{m}=\{\mathbf{p}_{k}\in P\ |\ L_{min,m} \leq p_{k} < L_{max,m} \}\]
  • $L_{min,m}$, $L_{max, m}$ : $Z_{m}$의 최소, 최대 반지름 경계


각 bin $S_{i, j,m}$은 다음과 같이 나타낼 수 있음

\[S_{i, j, m}=\{ \mathbf{p}_{k}\in Z_{m} \ | \frac{(i-1)\cdot\Delta L_{m}}{N_{r, m}} \leq \rho_{k}-L_{min, m} < \frac{i\cdot\Delta L_{m}}{N_{r, m}},\\ \frac{(j-1)\cdot2\pi}{N_{\theta, m}}-\pi \leq \theta_{k}< \frac{j\cdot2\pi}{N_{\theta, m}}-\pi \}\]
  • $N_{r, m}$ : $m$ 번째 zone의 ring의 수
    • 해당 Zone을 반지름 관점으로 몇 개로 나눌 것인지
  • $N_{\theta, m}$ : $m$ 번째 zone의 sector의 수
    • 해당 Zone을 radian 각도를 관점으로 몇 개로 나눌 것인지
  • $\Delta L_{m}=L_{max,m}-L_{min, m}$
  • $\rho_{k}$ $=$ \(\sqrt{ x^{2}_{k} + y^{2}_{k}}\)
  • $\theta_{k}=arctan2(y_{k}, x_{k})$


$L_{max,m}$은 $L_{min,m+1}$ 과 같음_

$L_{max,4}=L_{zmax}$, $L_{min,1}=L_{min}$ 이며 각각 global maximum boundary, global minimum boundary 라고 함

$L_{min}$은 움직이는 물체나 차량 주변의 비어있음을 고려하는데 사용됨..

  • 무슨말이지…

$Z_1$, $Z_2$,$Z_3$, $Z4$는 각각 central zone, quater zone, half zone, and outer zone 이라고 부름


$Z_1$, $Z_4$의 bin 크기는 sparsity issue, representability issue 를 해결하기 위해 상대적으로 큼

표현력을 잃지않았고 이로 인해 normal vector를 잘 추정할 수 있게 되었음

또한 구역별로 서로 다른 bin 크기를 가지게 만들어 bin의 수를 줄여 빠르게 연산할 수 있게 만듦


Region-wise Ground Plane Fitting

RANSAC이 outlier 제거에는 훨씬 효과적이나 PCA가 outlier허용 범위 안의 성능에서 속도가 훨씬 빠름을 확인

  • PCA 방법은 전처리 과정으로 사용하기 더 좋음

그래서 PCA 방법을 이용하여 fitting 과정 진행


하나의 bin에서 $C\in \mathbb{R}^{3\times 3}$ 는 unit space에 존재하는 point cloud의 covariance matrix


\[C\mathbf{v}_{\alpha}=\lambda_{\alpha}\mathbf{v}_{\alpha}\]
  • $\alpha=1, 2, 3$
  • $\lambda_{1} \geq \lambda_{2} \geq \lambda_{3}$


가장 작은 고유값과 대응되는 고유 vector $\mathbf{v}_{3}$가 ground plane의 normal vector를 나타냄

\[\mathbf{n}=\mathbf{v}_{3}=[a,b,c]^{T}\]


각 plane의 상관계수 $d$는 아래와 같이 계산됨

\[d=-\mathbf{n}^{p}\mathbf{\bar{p}}\]
  • $\mathbf{\bar{p}}$ 는 unit space내 point cloud의 평균 point 값


$n$ 번째 bin을 $S_{n}$ 로 표기하고 $S_{n}$의 cardinality가 충분히 크다면 가장 낮은 높이의 point들이 초기의 seed 값으로 사용

실제로 가장 낮은 높이를 가진 각 bin들의 점들은 ground surface에 속할 가능성이 높음

초기의 ground point $\hat{G}^{0}_{n}$ 다음과 같이 얻을 수 있음

\[\hat{G}^{0}_{n}=\{ \mathbf{p}_{k}\in S_{n} \ |\ z(\mathbf{p}_{k}) < \bar{z}_{init} + z_{seed} \}\]
  • $\bar{z}_{init}$ : 전체 seed point들의 평균 $z$ 값
  • $z(\cdot)$ : point의 z값 반환


이를 초기값으로 이용하여 iterative하게 ground point 값들을 업데이트

아래와 같은 방법으로 update함

$l$ 번째 iteration의 추정된 ground point set을 $\hat{G}^{l}_{n}$ 이라고 표현

$\hat{G}^{l}_{n}$의 normal vector는 \(\mathbf{n}_{n}^{l}\) 는 위의 PCA 를 통하여 얻을수 있음

평면의 상관계수 $d_{n}^{l}$은 아래와 같은 식으로 계산

\[d_{n}^{l}=-(\mathbf{n}_{n}^{l})^{T}\bar{\mathbf{p}}_{n}^{l}\]
  • \(\bar{\mathbf{p}}_{n}^{l}\) : $\hat{G}^{l}_{n}$의 point들의 평균값


위에서 구한 값들로 $\hat{G}^{l+1}_{n}$은 다음과 같은 식으로 얻을수 있음

\[\hat{G}^{l+1}_{n}=\{ \mathbf{p}_{k}\in S_{n} \ |\ d_{n}^{l}-\hat{d}_{k} < M_{d} \}\]
  • $\hat{d}_{k} $ : \(-(\mathbf{n}_{n}^{l})^{T}\mathbf{p}_{k}\)
  • $M_{d}$ : 평면과의 distance margin 값

위의 과정을 반복하여 ground point를 구함


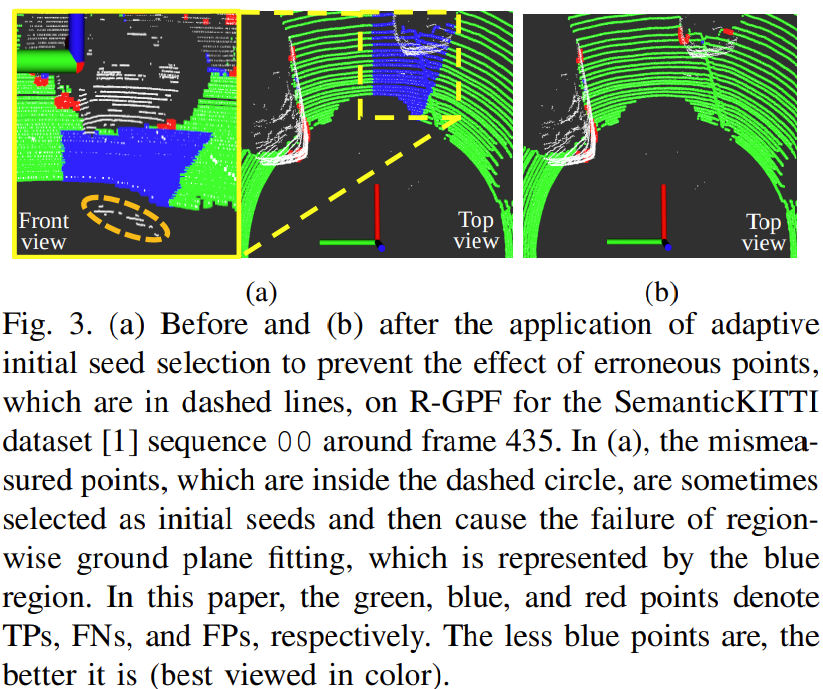
Screenshot from 2024-05-15 09-54-37


기존의 R-GPF와 다른점은 adaptive initial seed selection 사용한다는 점

Adaptive initial seed selection이 없으면 Multipath나 LiDAR 신호 반사 문제로 인해 실제 ground point보다 아래에 있는 잘못된 cloud point들이 얻어 질 수 있음 (Fig 3. (a))

이 현상은 $Z_{1}$ 에서 주로 발생

  • 신호가 비교적 강한 지역에서 반사가 발생되기 때문


이 문제를 해결하기 위해 $Z_{1}$에서만 ground point의 $z$ 값은 주로 센서의 높이, $h_{s}$ 근처에 있다는 사실 이용

따라서 $Z_{1}$에 속하는 bin $S_{n}$의 \(\hat{G}^{0}_{n}\)를 추정할 때, point \(\mathbf{p}_{k}\) $z_{k}$ 값이 $M_{h} \cdot h_{s}$ 인경우는 필터링함

  • $M_{h}<-1$은 height margin

$Z_{1}$에 속하지 않는 $S_{n}$의 경우, 부적절한 필터링을 막기 위해 $m$이 커질수록 adaptive threshold를 줄임


Ground Likelihood Estimation

앞의 과정에서 추정한 \(\hat{G}_{n}\) 가 실제의 ground point인지 식별하는 과정 필요


\[L(\theta \ | \ X)=f(X\ | \ \theta )= \prod _{n}f(X_{n} \ | \ \theta_{n})\]
  • $X$ : $\hat{G}_{n}$에서 밀도 함수 $f$ 를 가지는 연속 확률 분포를 따르는 random variable
  • $\theta$ : $\hat{G}_{n}$에서 Patchwork의 모든 파라미터


각 $\hat{G}_{n}$이 ground pointㅏ 될 가능성이 얼마나 있는지는 uprightness, elevation, flatness 관점에서 결정

\[f(X_{n} \ | \ \theta_{n})= \phi (\mathbf{v}_{3,n}) \cdot \psi(\bar{z}_{n}, r_{n}) \cdot \varphi(\psi(\bar{z}_{n}, r_{n}),\sigma_{n})\]
  • $\phi(\cdot )$ : uprightness
  • $\psi(\cdot )$ : elevation
    • $\bar{z}_{n}$ : $z$ 값의 평균
    • $r_{n}$ : 원점과 $S_{n}$의 중심점과의 거리
  • $\varphi(\cdot )$ : flatness
    • $\sigma_{n}$ : $\frac{\lambda_{3, n}}{\lambda_{1, n}+\lambda_{2, n}+\lambda_{3, n}}$


Screenshot from 2024-05-15 11-25-30


Uprightness

$\hat{G}_{n}$이 실제 ground의 속하는 경우(즉, 대부분이 TP인 경우), \(\mathbf{v}_{3}\)은 차량이 접촉해있는 ground에 직교할 가능성이 높음

즉, \(\mathbf{v}_{3}\)는 센서 프레임의 $X-Y$ 평면에 수직인 경향이 있음

따라서 uprightness는 아래의 식으로 계산 가능

\[\phi (\mathbf{v}_{3,n})=\left\{\begin{aligned} &1, \ if\ \frac{\mathbf{v}_{3, n}\cdot \mathbf{z}}{\left\| \mathbf{v}_{3, n} \right\| \ \left\|\mathbf{z} \right\|} > cos(\frac{\pi}{2}-\theta_{\tau})\\ &0, \ otherwise \end{aligned}\right.\]

  • \(\mathbf{z}\) : $[0 \ 1 \ 1]$

  • $\theta_{\tau}$ : uprightness margin

Uprightness margin을 사용하여 직교가 아닌 각도가 어느 정도 범위 안에 들어오더라도 uprightness 하다고 간주

Fig 4.(a), (b)의 빨간 영역은 uprightness가 만족하지 않는 영역을 나타냄


Elevation

Uprigghtness 만으로는 $\hat{G}_{n}$이 자동차의 보넷이나 천장등을 필터링하기 하는 것은 불가능함

자동차와 같은 큰 물체가 센서 프레임에 가까우면, Occlusion이 발생하고 이로 인한 부분적인 관찰 이슈가 발생

즉, occlusion이 존재하는 공간에서의 point cloud은 공간의 가장 낮은 부분이 아닌 $\hat{G}_{n}$으로 예측

  • 이 부분 내용이 이해가 안감…

Fig 4.(a)에서 이 현상 관찰 가능


이러한 문제를 해결하기 위해, elevation filter 적용

센서 프레임 근처의 \(\bar{z}_{n}\) 값이 센서의 높이 $h_{s}$ 대비 많이 높다면 $\hat{G}_{n}$은 ground가 아닐 가능성이 높음

  • Fig. 4(c)에서 확인 가능

Uprightness만을 사용한다면, $r_{n}$이 작은 경우, TP의 약간의 손실이 있지만 $\bar{z}_{n}$을 기준으로 TP와 FP를 구별 가능

  • $Z_{1}$, $Z_{2}$에서의 $\hat{G}_{n}$

하지만 $r_{n}$이 클 때는 TP와 FP를 구별 할 수 없음

  • $Z_{4}$에서의 $\hat{G}_{n}$


이 관찰을 바탕으로 다음과 같이 elevation 측정

\[\psi(\bar{z}_{n}, r_{n})= \left\{\begin{aligned} &(1+e^{(\bar{z}_{n}-k(r_{n}))})^{-1}, \ if\ r_{n} < L_{\tau} \\ &1, \ otherwise \end{aligned}\right.\]
  • $k(\cdot)$ : adaptive midpoint function, $r_{n}$에 따라 지수적으로 증가
  • $L_{\tau}$ : range parameter 상수


Flatness

Flatness의 목적은 elevation으로 필터링 된 FN들이 확실하게 균일한 평면인 경우 이를 되돌리는 것

$\hat{G}_{n}$이 아주 가파른 오르막에 속해있으면 \(\bar{z}_{n}\) 은 $k(r)$ 보다 값이 크기 때문에 elevation에서 필터링이 됨

이 문제를 해결하기 위해 surface variable $\sigma_{n}$ 을 사용하여 \(\psi(\bar{z}_{n}, r_{n})\) 값이 0.5보다 낮더라도 FN으로 생각되는 $\hat{G}_{n}$의 flatness를 확인

아래와 같이 정의하여 확인

\[\varphi(\psi(\bar{z}_{n}, r_{n}),\sigma_{n})=\left\{\begin{aligned} &(\zeta e^{-(\sigma_{n}-\sigma_{\tau,m})}, \ if \ \psi(\bar{z}_{n}, r_{n})<0.5 \\ &1, \ otherwise \end{aligned}\right.\]



EXPERIMENTS

Screenshot from 2024-05-15 12-44-22

  • 기존 benchmark인 ERASOR (R-GPF 방식) 보다 향상된 성능을 확인


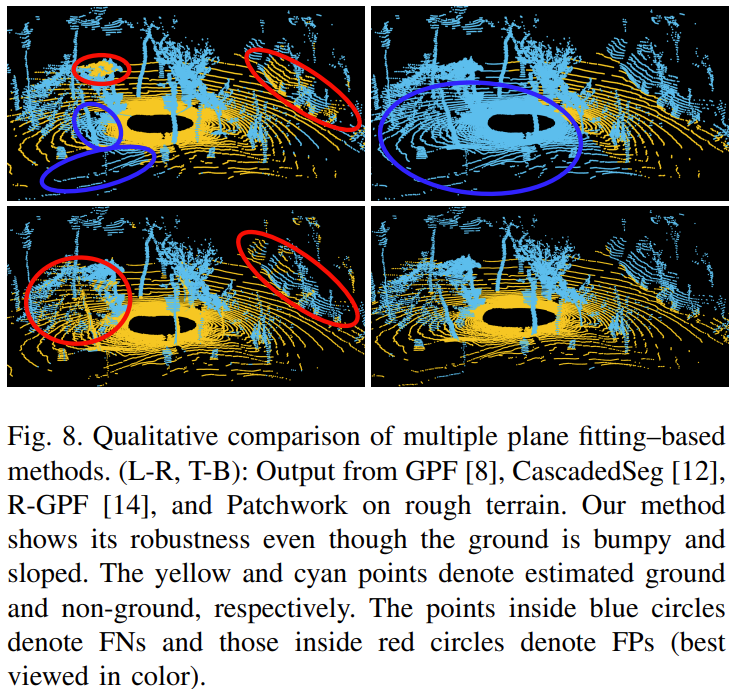
Screenshot from 2024-05-15 12-45-22

  • 기존 방법론들과 비교하여 FP 결과가 줄어든 것을 확인


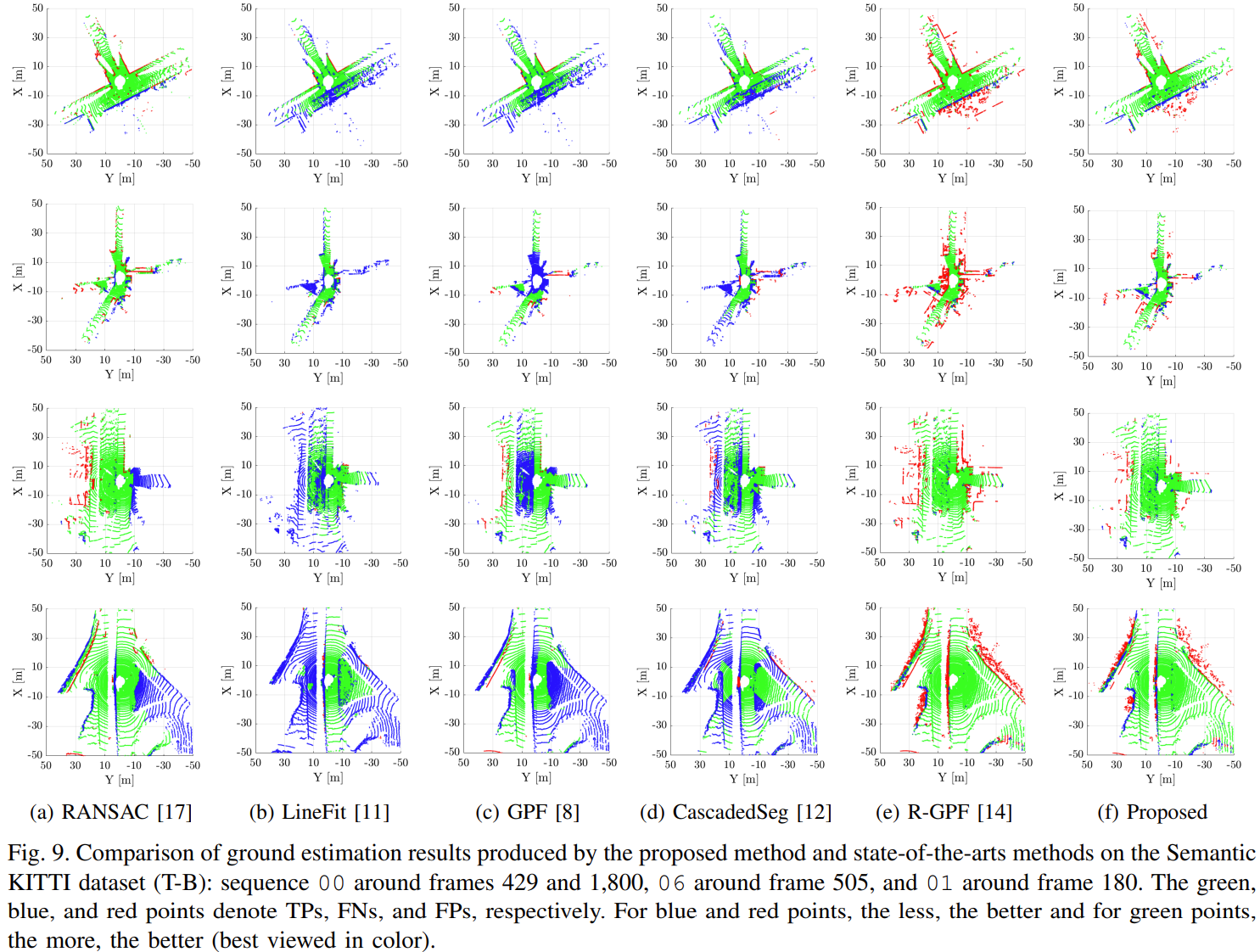
Screenshot from 2024-05-15 12-52-15

  • Ground 영역 다른 방식들보다 잘 구별함을 확인


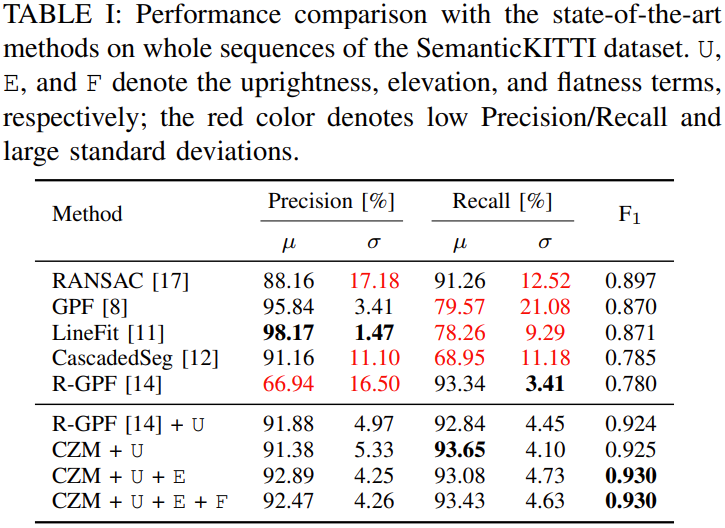
Screenshot from 2024-05-15 12-53-45

  • Precision과 Recall이 모두 안정적으로 좋은 결과 도출
  • LineFit의 경우 Precision은 높으나 Recall 값이 낮음



Conclusion

빠른 연산과 향상된 정확도를 가지는 ground segmentation 방법 제공

CZM 기반으로 bin 크기를 적절하게 조정하여 계산 복잡도를 줄임

Likelihood 기반으로 FP 감소

기존의 Region-wise ground plane fitting 방식 이용

참고