Complex-YOLO
참고
Complex-YOLO: An Euler-Region-Proposal for Real-time 3D Object Detection on Point Clouds
2018
Introduction
이미지와 다르게, Lidar point cloud 데이터는 전체 측정 범위에서 다양한 density를 가지며 sparse함
또한 데이터의 순서가 없고, 지역적으로 상호 작용을하고, 분리하여 분석을 할 수 없음
Point cloud processing은 항상 기본 변환에 불변해야 함
딥러닝 연구는 정확도(accuracy)와 효율성(efficiency)의 trade-off가 매우 중요한데, 자율 주행에서는 효율성이 더 중요함
그래서 최적의 object detector는 RPN (Region Proposal Network) 이나 grid를 기반으로한 RPN을 사용한 방법
이러한 네트워크는 매우 효율적이고, 정확하며 또한 전용 하드웨어나 임베디드 장치에서도 사용이 가능
Point cloud를 이용한 object detection 연구는 드물지만 점점 중요해지고 이를 통해 3D bounding box를 예측을 가능하게 해줌
현재는 딥러닝을 이영한 방법으로는 3가지 주요한 방법이 존재
- MLP을 이용하여 직접적으로 point cloud를 이용하는 방법
- Point cloud를 voxel이나 image stack으로 만들어 CNN을 적용하는 방법
- 결합된 fusion 방법
Contribution
자율 주행 측면에서, 실시간으로 작동하는 효율적인 object detection 방법이 없었음
우리는 NVIDIA Titan GPU에서 50 fps보다 빠르게 동작하는 slim하고 정확한 모델 소개
Point cloud 전처리와 feature 추출을 위해 multi-view idea를 사용 (MV3D)
하지만 multi-view fusion은 사용하지 않고 LiDAR를 사용하여 하나의 birds-eye view RGB-map을 생성함
가장 빠른 SOTA의 이미지 detector YOLOv2의 3D 버전인 Complex-YOLO 제시
Complex-YOLO는 E-RPN을 사용하여 각 box의 실수 허수 부분으로 코드화된 객체의 방향을 추정
Complex-YOLO는 3D box의 정확한 위치와 방향을 실시간으로 예측 가능하고, 적은 수의 point를 가지는 pedestrian의 같은 경우도 예측이 가능함
아래는 이 논문의 주요 contribution
- E-RPN을 사용하는 Complex-YOLO를 이용하여 신뢰할 수 있는 3D box regression 결과를 얻을 수 있음
- KITTI benchmark 데이터로 평가했을 때 높은 정확도로 실시간 성능 제시
- 주변 객체의 궤적을 예측할수 있는 E-RPN을 이용하여 3D bounding box의 정확한 방향을 예측
- 다른 Lidar 기반 방식들과 비교했을 때, 모든 class들을 한 번에 모든 class들을 예측을 잘 할 수 있음
Complex-YOLO
Grid 기반의 point cloud 전처리 방식, 특정 network architecture , 학습을 위한 loss function과 실시간 성능을 보장하기 위한 효율적인 설계(design)에 대해 설명
Point Cloud Preprocessing
Velodyne HDL64 laser scanner에서 얻은 한 프레임에 대한 3D point cloud는 하나의 birds-eye-view RGB-map으로 변환
센서의 원점 바로 앞의 $80m \times 40m$ 영역 $\Omega$의 Point cloud $P_{\Omega} \in \mathbb{R}^{3}$ 만 사용
- 가로 $80m$, $-40m \sim 40m$
- 세로 $40m$, $0 \sim 40m$
Grid map의 크기는 $n=1024, m=512$, 즉 $1024 \times 512$
따라서, 3D point cloud를 약 $g=8cm$의 해상도를 가진 2D grid로 projection 하고 나눔
\(S_{j}=f_{PS}(P_{\Omega_{j}},g)\)는 $\Omega$ 영역에 존재하는 point cloud $i$를 한 pixel이 대략 $g=8cm$인 gird map $j$로 mapping 하는 것을 의미
Grid $j$에는 맵핑된 여러 point 존재
\[P_{\Omega_{i} \rightarrow j}=\{P_{\Omega_{i}}=[x,y,z]^{T}|S_{j}=f_{PS}(P_{\Omega_{j}},g)\}\]각 Gid, 즉 pixel의 채널 계산
$S_{j}$에 존재하는 여러 point들 중에서 가장 큰 height 값을 $z_{g}(S_{j})$으로 인코딩
$S_{j}$에 존재하는 여러 point들 중에서 가장 intensity 값이 큰 값을 $z_{b}(S_{j})$로 인코딩
$S_{j}$에 존재하는 여러 point들의 수, 즉 density를 normalize 한 값을 $z_{r}(S_{j})$로 인코딩
\[\begin{align*} &z_{g}(S_{j})=max(P_{\Omega_{i} \rightarrow j}\cdot[0,0,1]^{T})\\ &z_{b}(S_{j})=max(I(P_{\Omega_{i} \rightarrow j})) \\ &z_{r}(S_{j})=min(1.0,\log(N+1)/64) \ \ N=|P_{\Omega_{i} \rightarrow j}| \end{align*}\]Architecture
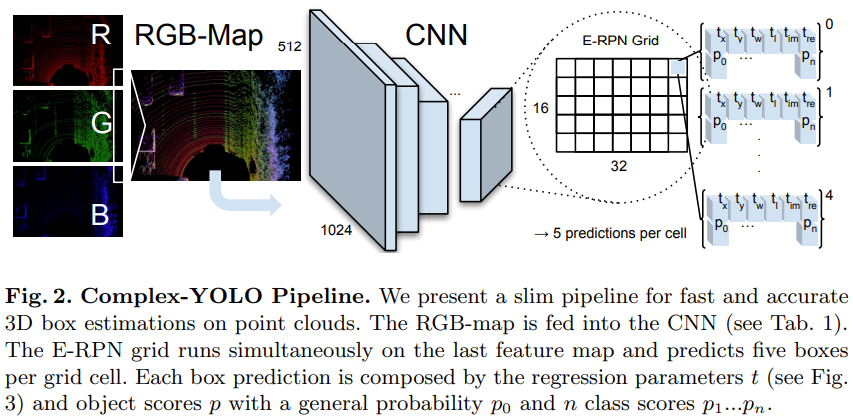
Complex-YOLO 네트워크는 birds-eye-view RGB map 입력으로 사용
- $1024\times 512 \times \ 3$
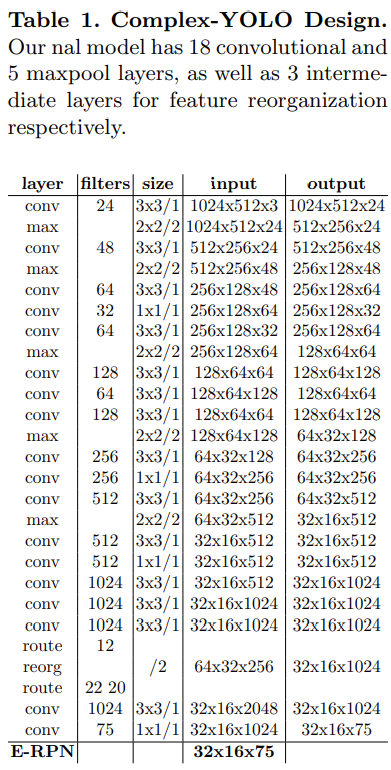
YOLO 모델의 output은 $32 \times 16 \times 75$
- 한 grid 당 5개의 anchor box가 나오고 각 anchor box당 15개의 값 존재
- Box의 위치, 크기, 각도 $t_{x}, t_{y},t_{w}, t_{l}, t_{Im}, t_{Re}$ (6개)
- confidence score $p_{0} $(1개)
- class probability $p_{1}, p_{2}, p_{3}$(3개)
- E-RPN parameter $\alpha, c_{x}, c_{y}, p_{w}, p_{l}$
E-RPN은 YOLO의 output을 input으로 사용
Complex angle regression 과 E-RPN으로 확장한, 단순한 YOLOv2 CNN architecture 사용하여 실시간으로 multi-class의 방향을 가진 3D bounding box를 감지
Euler-Region-Proposal
E-RPN은 Input으로 들어오는 feature map에서 3D box의 object의 위치, 크기 방향을 얻기 위한 network
- 위치 : $b_{x}$, $b_{x}$
- 크기 : $b_{w}$, $b_{l}$
- 방향 : $b_{\phi }$ , 이 것을 complex angle로 나타냄
| 적절한 방향을 얻기 위해 Grid-RPN에 complex angle $arg(\left | z\right | e^{ib_{\phi}})$을 추가하여 수정 |
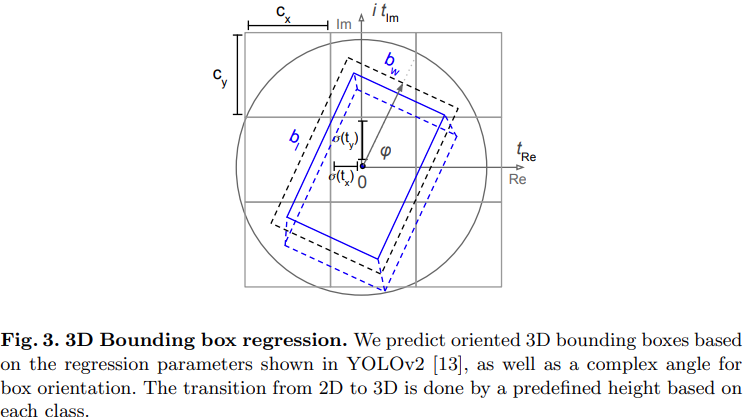
E-RPN은 네트워크에 직접 포함된 허수 및 실수 분수를 기반으로 정확한 물체 방향을 추정
E-RPN의 output은 $32 \times 16 \times 50$
-
한 grid 당 5개의 anchor box가 나오고 각 anchor box당 10개의 값 존재
-
Box의 위치, 크기, 각도
-
confidence score $p_{0} $(1개)
-
class probability $p_{1}, p_{2}, p_{3}$(3개)
-
Anchor Box Design
각 Grid cell에서 5rodml box 예측
Angle regression이 추가되었기 때문에 prior anchor box의 수를 늘릴 수도 있었지만 효율성 때문에 늘리지 않고 5개로 제한
따라서 3개의 다른 크기와 2개의 각도로 prior를 구성
- vehicle size (heading up)
- vehicle size (heading down)
- cyclist size (heading up)
- cyclist size (heading down)
- pedestrian size (heading left)
Loss Function
Loss는 아래와 같은 식으로 계산
\[L=L_{\text{Yolo}}+L_{\text{Euler}}\]$L_{\text{Yolo}}$는 아래와 같이 일반적인 YOLO의 loss 함수
\[\begin{split} L_{\text{Yolo}}= & \lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} \left[ (x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2 \right] \\ & +\lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} \left[ (\sqrt{w_i} - \sqrt{\hat{w}_i})^2 + (\sqrt{h_i} - \sqrt{\hat{h}_i})^2 \right] \\ & + \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} (C_i - \hat{C}_i)^2 \\ & + \lambda_{\text{noobj}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{noobj}} (C_i - \hat{C}_i)^2 \\ & + \sum_{i=0}^{S^2} \mathbb{1}_i^{\text{obj}} \sum_{c \in \text{classes}} (p_i(c) - \hat{p}_i(c))^2 \end{split}\]$L_{\text{Euler}}$ 는 complex angle의 각각에 대한 차이의 제곱으로 계산
\[\begin{align*} L_{\text{Euler}}&=\lambda_{coord} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} \left| (e^{ib_{\phi }}-e^{i\hat{b}_{\phi }} )^{2}\right| \\ &=\lambda_{coord} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}}[(t_{im}-\hat{t}_{im})^{2}+(t_{re}-\hat{t}_{re})^{2}] \end{align*}\] \[\begin{split} L_{\text{Yolo}}= & \lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} \left[ (x_i - \hat{x}_i)^2 + (y_i - \hat{y}_i)^2 \right] \\ & +\lambda_{\text{coord}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} \left[ (\sqrt{w_i} - \sqrt{\hat{w}_i})^2 + (\sqrt{h_i} - \sqrt{\hat{h}_i})^2 \right] \\ & + \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{obj}} (C_i - \hat{C}_i)^2 \\ & + \lambda_{\text{noobj}} \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{\text{noobj}} (C_i - \hat{C}_i)^2 \\ & + \sum_{i=0}^{S^2} \mathbb{1}_i^{\text{obj}} \sum_{c \in \text{classes}} (p_i(c) - \hat{p}_i(c))^2 \end{split}\]